
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Исследование операций. Линейное программирование.
Найти максимум и минимум линейного функционала Y (`x)= -x1 + 3x2 при условиях
Y=4X1+6X2
 | |||
 | |||
9x1- 2x2 ³ 0 9x1- 2x2 = 0 (1)
x1 + x2 £ 8 уравнения x1 + x2 = 8 (2)
 -x1 + 3x2 ³ -6 границ -x1 + 3x2 = -6 (3)
-x1 + 3x2 ³ -6 границ -x1 + 3x2 = -6 (3)
5x1 + 3x2 ³ 15 множества 5x1 + 3x2 = 15 (4)
x1 ³ 0; x2 ³ 0 x1 = 0; x2 = 0

Исходное положение функционала
Y=0
-x1 + 3x2 = 0
3x2 = x1 ; x2 = 1/3 x1
При x1 = 3 x2 = 1










(1)x2= 4,5x1; (3)x1 =0; x2 =-2
x1 =1; x2 =4,5 x1 =6; x2 =0
x1 =2; x2 =9 x2 =1/3x1 –2
гиперплоскость гиперплоскость сверху
снизу
(2)x1 =0; x2 =8 (4)x1 =0; x2 =5
x1 =8; x2 =0 x1 =3; x2 =0
x1=0; x2 =0 x1 =0; x2 =0
гиперплоскость гиперплоскость сверху
снизу
Для поиска в множестве экстремальных значений необходимо исходный функционал Y=0 подвергнуть аффинному преобразованию, что в системе координат соответствует пропорциональному изменению координат по всем осям (примечание: так натуральная фигура превращается в её модель и наоборот). В нашем двумерном случае (x1 и x2) соответствует параллельному переносу линии Y=0 до крайней верхней точки С (это максимум и до крайних нижних точек линии ED (это минимум). Примечание: координаты любой точки линии ED равноценны, так как ED║Z(0).
1) Вычислим Zmax, для чего:
а) определим координаты точки С, как пересечение прямых (1) и (2)

 =
= 

 =
= 


 =
= 


Проверка: 9·1,45-2·6,54=13,08-13,08=0
Zmax = -1,45+3·6,54 = 18,17
2)Вычислить Zmin, для чего:
а) определим координаты точки D, как пересечение прямых (2) и (3)

 =
= 

 =
= 


 =
= 


Проверка: 7,5+0,5=8

Б) Проконтролируем  , подставив координаты т. E(6;0)
, подставив координаты т. E(6;0)

Таким образом, оптимальный план задачи:
1)  =18,17 при
=18,17 при 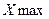 =(1,45;6,54)
=(1,45;6,54)
2)  =-6 при
=-6 при 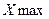 =[
=[  ]
]
Дата добавления: 2015-01-05; просмотров: 280; Мы поможем в написании вашей работы!; Нарушение авторских прав |