Студопедия

КАТЕГОРИИ:

АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника


Решение типовых примеров.

⇐ ПредыдущаяСтр 57 из 58Следующая ⇒



1. Правильной записью числа в тринадцатиричной системе счисления является…

а) 5D631 б) 1F3B0
в) 1EB27 г) 2C5A

Решение:

Так как тринадцатиричная система счисления, это система счисления с основанием 13, цифры, используемые в записи числа от 0 до 9, А – 10,
B – 11, C – 12, то правильной записью числа в тринадцатиричной системе счисления является число г) 2C5A.

Ответ: г) 2C5A.

2. Среди перечисленных чисел максимальным является...

а) 22010 б) 110101012
в) DA16 г) 2478

Решение:

Переведем числа б) 110101012, в) DA16, г) 2478 в десятичную систему счисления, для этого запишем числа в развернутой форме записи и вычисляя выражение развернутой формы записи получим десятичный эквивалент указанного числа.

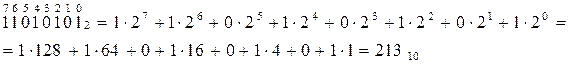
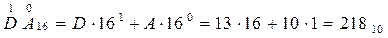
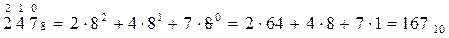
Следовательно, среди указанных чисел максимальным является число 22010.

Ответ: а) 22010.

3. Переведите данные числа из десятичной системы счисления
а), б) в двоичную, в) восьмеричную и г) шестнадцатеричную системы счисления.

а) 75310 б) 193,974810 с точностью до 2-8
в) 83510 г) 65110

Решение:

а) 75310

При переводе числа десятичной системы в двоичную целая часть переводится путем деления на 2 с записью остатков от деления до тех пор, пока частное не будет равно 0. Собрав все остатки от деления, снизу вверх, мы получаем код числа.

                 
               
1              
  0            
    0          
      0        
        1      
          1    
            1  
              1
                0
                  1  

Получаем: 75310=10111100012


б) 193,9748 с точностью до 2-8.

Переводим целую часть:

               
             
1            
  0          
    0        
      0      
        0    
          0  
            1
              0
                1  

19310=1010000012

Переводим дробную часть:

Дробная часть кодируется путем умножения дробной части на 2 с переносом целой части от умножения в левую колонку до тех пор, пока дробная часть произведения не станет равной 0 или не будет достигнута требуемая точность представления числа, код числа получается путем сбора целых частей сверху вниз.

1

0,974810=0,111110012

Получаем:193,974810= 101000001,111110012

в) 83510

При переводе числа десятичной системы в восьмеричную целая часть переводится путем деления на 8 с записью остатков от деления до тех пор, пока частное не будет равно 0. Собрав все остатки от деления, снизу вверх, мы получаем код числа.

     
   
3  
  0
    5
      1  

Получаем: 83510=15038

г) 65110

При переводе числа десятичной системы в шестнадцатеричную целая часть переводится путем деления на 16 с записью остатков от деления до тех пор, пока частное не будет равно 0. Собрав все остатки от деления, снизу вверх, мы получаем код числа.

   
 
11(B)
8
    2  

Получаем: 65110=28B16

Ответ: а)75310=10111100012; б) 193,974810= 101000001,111110012;
в)83510=15038; г) 65110=28B16.

4.Переведите данное число в десятичную систему счисления.

а) 1110100102 б) 2307,58
в) 11011100,0112 г) 1Е9А16

Решение:

Для перевода чисел в десятичную систему счисления, запишем числа в развернутой форме записи и вычислим выражение развернутой формы записи получим десятичный эквивалент указанного числа.

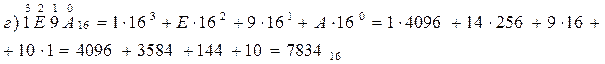
Ответ: ; ;

; .

5.Выполните действия.

а) 1010011,1112+11001,1102 д) 540178+367168
б) 10111001,12 - 10001101,12 е) 10348-7658
в) 11001,012 × 11,012 ж) С9A16+B1D16
г) 1010001012 : 11012 з) А3D16-6BF16

Решение:

а) 1010011,1112+11001,1102=1101101,1012

 

+ 1,
    1,
  1,

б) 10111001,12 - 10001101,12 = 101100,02

          , ,        
-   1,
  1,
    0,

в) 11001,012 × 11,012 = 1010010,00012

×       1,
            1,
       
       
       
0,

 

 

г) 1010001012 : 11012 = 110012

-  
         
    -                
                   
          -          
                   
                           

д)540178+367168=1127358

+

е) 10348-7658=478

-
 
     

ж) С9A16+B1D16=17B716

+   C A
  B D
  B

з) А3D16-6BF16=37E16

- A D
B F
  E

Ответ: а)1010011,1112+11001,1102=1101101,1012;

б) 10111001,12 - 10001101,12 = 101100,02;

в) 11001,012 × 11,012 = 1010010,00012;

г) 1010001012 : 11012 = 110012;

д)540178+367168=1127358;

е) 10348-7658=478;

ж) С9A16+B1D16=17B716;

з) А3D16-6BF16=37E16.


11. Правильной записью числа в троичной системе счисления является…

а) 102631 б) 103B0
в) 11002 г) 25

12. Правильной записью числа в четверичной системе счисления является…

а) 110302 б) 10340
в) 1A002 г) 35

13. Правильной записью числа в пятеричной системе счисления является…

а) 102611 б) 10340
в) 1A002 г) 25

14. Правильной записью числа в шестеричной системе счисления является…

а) 102611 б) 12052
в) 120В2 г) 257

15. Правильной записью числа в семеричной системе счисления является…

а) 12645 б) 10349
в) 130F2 г) 257

16. Правильной записью числа в восьмеричной системе счисления является…

а) 902611 б) 4562
в) F3401 г) 249

17. Правильной записью числа в девятеричной системе счисления является…

а) 1D026 б) 19452
в) 80327 г) 2A5

18. Правильной записью числа в одинадцатеричной системе счисления является…

а) 45C б) 2A9B
в) 2B50 г) 1A002

19. Правильной записью числа в двенадцатеричной системе счисления является…

а) A261F б) 704B
в) 1C5 г) 2DA

20. Правильной записью числа в четырнадцатеричной системе счисления является…

а) 4CD б) EB340
в) 3A00F г) 25E

21. Среди перечисленных чисел максимальным является...

а) 24510 б) 111101112
в) EF16 г) 3468

22. Среди перечисленных чисел максимальным является...

а) 16410 б) 101111112
в) AF16 г) 1568

23. Среди перечисленных чисел максимальным является...

а) 34210 б) 111011112
в) ED16 г) 2568

24. Среди перечисленных чисел максимальным является...

а) 50410 б) 10011112
в) 5F16 г) 1268

25. Среди перечисленных чисел максимальным является...

а) 21010 б) 110111112
в) D716 г) 1478

26. Среди перечисленных чисел максимальным является...

а) 17410 б) 111101002
в) B416 г) 2378

27. Среди перечисленных чисел максимальным является...

а) 32410 б) 110001012
в) C716 г) 2168

28. Среди перечисленных чисел максимальным является...

а) 15910 б) 110010112
в) A716 г) 5048

29. Среди перечисленных чисел максимальным является...

а) 45210 б) 111101002
в) D316 г) 5028

30. Среди перечисленных чисел максимальным является...

а) 38010 б) 110101112
в) AB16 г) 1548

 

Переведите данные числа из десятичной системы счисления
а), б) в двоичную, в) восьмеричную и г) шестнадцатеричную системы счисления:

31.

а) 86010 б) 149,376310 с точностью до 2-5
в) 78510 г) 95310

32.

а) 65110 б) 243,478310 с точностью до 2-5
в) 47210 г) 87310

33.

а) 43910 б) 512,753110 с точностью до 2-5
в) 60210 г) 49310

34.

а) 53210 б) 367,607510 с точностью до 2-5
в) 32710 г) 79110

35.

а) 93110 б) 602,173210 с точностью до 2-5
в) 45710 г) 56910

36.

а) 74510 б) 723,367510 с точностью до 2-5
в) 93710 г) 49610

37.

а) 27510 б) 549,419710 с точностью до 2-5
в) 78510 г) 82710

38.

а) 49910 б) 741,127410 с точностью до 2-5
в) 70110 г) 75510

39.

а) 38910 б) 498,702310 с точностью до 2-5
в) 67310 г) 48510

40.

а) 76610 б) 553,144710 с точностью до 2-5
в) 40310 г) 871

 

Переведите данное число в десятичную систему счисления:

41.

а) 10010102 б) 775,28
в) 111111100,00012 г) A9416

42.

а) 11101012 б) 3248
в) 10110111,0112 г) 7B416

43.

а) 11011112 б) 407,18
в) 10001110,01012 г) 34F16

44.

а) 10111102 б) 6218
в) 10010001,1012 г) 5FD16

45.

а) 11100102 б) 250,48
в) 11011111,112 г) F4E16

46.

а) 10101012 б) 424,28
в) 11101110,01012 г) 8E916

47.

а) 10010002 б) 252,48
в) 10111111,11012 г) 2DA16

48.

а) 11110112 б) 671,28
в) 10101111,0112 г) E3A16

49.

а) 10011012 б) 531,48
в) 10011111,1112 г) F9C16

50.

а) 10000012 б) 704,28
в) 10111100,1012 г) 56F16

 

Выполните действия:

51.

а) 101011,112+1110,12 д) 534128+257068
в) 11010,012-1110,112 е) 7038-2148
б) 10112 11012 ж) D216+F16
г) 10100112:10112 с точностью до 2-3 з) C389616-845FA16

52.

а) 110111,012+1010,12 д) 3418+7068
в) 10110,012-1100,112 е) 720478-435768
б) 11012 10112 ж) F7983216+C9A5316
г) 11010112:11012 с точностью до 2-3 з) C916-A16

53.

а) 101111,112+1011,012 д) 420768+204658
в) 10110,012-1010,112 е) 6458-3268
б) 11112 10012 ж) E716+D16
г) 10100112:10012 с точностью до 2-3 з) F38A616-945DA16

54.

а) 111011,112+1010,12 д) 4128+7368
в) 11011,012-1010,012 е) 567038-241568
б) 10112 10112 ж) 2A5D216+12F416
г) 10110112:10112 с точностью до 2-3 з) C9816-54A16

55.

а) 111110,112+1010,012 д) 427618+575048
в) 10010,012-1111,012 е) 5738-3758
б) 10002 10112 ж) 59BE316+4F5616
г) 10111012:11102 с точностью до 2-3 з) D716-B16

56.

а) 101010,112+10110,12 д) 7448+5768
в) 10011,012-1011,12 е) 711038-253148
б) 11012 10012 ж) E216+F16
г) 10111112:11012 с точностью до 2-3 з) D78A116-61F6316

57.

а) 100111,112+1010,12 д) 431278+340168
в) 11110,012-1010,112 е) 7128-3148
б) 11112*11012 ж) C916+E16
г) 10110112:10102 с точностью до 2-3 з) 5D47F16-315BA16

58.

а) 101111,112+1111,012 д) 6318+5778
в) 11011,012-1110,112 е) 756038-271048
б) 10012 10112 ж) D45F216+56A816
г) 10110112:11112 с точностью до 2-3 з) D916-A16

59.

а) 101011,112+1010,12 д) 5037648+407768
в) 10011,112-1110,112 е) 6748-3658
б) 10112 11112 ж) E216+F16
г) 10111112:10012 с точностью до 2-3 з) B4E4516-46F5A16

60.

а) 101010,112+11111,012 д) 6778+5638
в) 11110,112-1110,112 е) 707458-261478
б) 11112 10012 ж) B639116+F6A316
г) 11110112:11112 с точностью до 2-3 з) F716-C16

Литература:

1.Информатика: Учебник / Под ред. Н.В.Макаровой. - 3-е изд., перераб. - М. : Финансы и статистика, 2004. - 765 с.

2.Информатика для юристов и экономистов: Учебник для вузов / под ред. С.В. Симоновича – СПб: Питер, 2006. – 687 с.

3.Острейковский В.А. Информатика: Учебник для вузов.- М.: Высш. шк., 1999.- 511 с.

4.Акулов О.А. Информатика: базовый курс. – М.: Омега-Л, 2005. – 552с.

5.Информатика и математика для юристов : Учебник / Под ред. С.Я. Казанцева, Н.М. Дубининой. - 2-е изд., перераб. и доп. - М. : ЮНИТИ-ДАНА, 2006. - 560с.

 

Тема 3: Логические основы ЭВМ.

Поделиться:

Дата добавления: 2015-01-05; просмотров: 1002; Мы поможем в написании вашей работы!; Нарушение авторских прав

⇐ Предыдущая49505152535455565758Следующая ⇒
lektsii.com - Лекции.Ком - 2014-2025 год. (0.007 сек.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав
Главная страница Случайная страница Контакты