Описание экспериментальной установки

ПОСІБНИК

для самостійної роботи

та практичних занять
з НАВЧАЛЬНОЇ ДИСЦИПЛІНИ

“РЕЛІГІЄЗНАВСТВО”

галузь знань 0304 “Право”, 0302 “Міжнародні відносини”;

напрям підготовки 6.030401 “Правознавство”,

6.030202 “Міжнародне право”;

освітньо-кваліфікаційний рівень “Бакалавр”

для студентів І курсу денної форми навчання

У к л а д а ч і: Юркевич Олена Миколаївна,

Качурова Світлана Володимирівна

Відповідальний за випуск О. М. Юркевич

Лабораторная работа № M-4

ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА ИЗ ПРОГИБА СТЕРЖНЯ

Цель работы

Целью работы является изучение зависимости прогиба стержня от величины действующей на него силы; определение модуля Юнга материала стержня.

Оборудование и принадлежности

Прибор для определения модуля Юнга, набор грузов.

Теоретическая часть

Основные понятия и определения

Деформация – изменение относительного положения частиц тела, связанное с их перемещением. Все реальные тела под действием сил изменяют свою форму и размеры, т. е. деформируются.

Деформации разделяют на упругие и пластические.

Упругие деформации – это деформации, исчезающие после снятия нагрузки. Т.е. после прекращения действия силы тело принимает первоначальные форму и размеры. В основе упругих деформаций лежат обратимые смещения атомов вещества от положения равновесия

Пластические деформации – это деформации, которые остаются после окончания действия приложенных сил. В основе пластических деформаций лежат необратимые перемещения атомов на значительные расстояния от исходных положений равновесия.

Наиболее простые виды деформации тела в целом:

- растяжение,

- сжатие,

- сдвиг,

- изгиб,

- кручение.

В теории упругости доказывается, что все виды деформаций могут быть сведены к одновременно происходящим деформациям растяжения (сжатия) и сдвига.

Рассмотрим простейшую деформацию продольного растяжения (рисунок 1). К концам однородного стержень длиной l с площадью поперечного сечения S приложены силы и 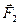. В результате действия этих сил длина стержня меняется на величину l.

l – абсолютное удлинение стержня;

– относительное удлинение (относительная деформация).

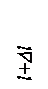
Рисунок 1 – Схема продольного растяжения

Сила, действующая на единицу площади поперечного сечения, называется напряжением:

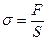. (1)

Если сила направлена по нормали к по­верхности, напряжение называется нор­мальным,если же по касательной к по­верхности — тангенциальным.

Закон Гука: для малых деформаций относительное уд­линение e прямо про­порционально вызывающему его напряжению s:

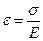(2)

где Е – коэффициент пропорциональности, называется модулем Юнга.

Физический смысл модуля Юнга: модуль Юнгачисленно равен напряжению, вызывающему относительное удлинение, равное единице. При относительном удлинении, равном единице , абсолютное удлинение l = l, откуда получаем: модуль Юнга численно равен тому напряжению, которое растягивает стержень вдвое. На самом деле большинство материалов разрушается раньше, чем они будут растянуты вдвое, поэтому фактически нельзя приложить к стержню напряжение численно равное модулю Юнга.

Выразим относительное удлинение с учетом (1) и (2): 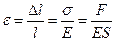, отсюда или

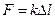,(3)

где k – коэффициент упругости.

Выражение (3) также задает закон Гука: при упругой деформации абсолютное удлинение стержня пропорционально действующей силе.

Закон Гука справедлив только при невысоких напряжениях. При больших напряжениях закон Гука нарушается. Связь между деформацией и напряжением представляется в виде диаграммы напряжений (рисунок 2).

Рисунок 2 – Диаграмма напряжений малоуглеродистой стали

Из рисунка видно, что линейная зависимость s (e), установленная Гуком, выполняется лишь в очень узких пределах до так называемого предела пропорциональности(s_п). При дальнейшем увеличении напряжения деформация еще упругая (хотя зависимость s (e) уже не линейна) и до предела упругости(s_у) остаточные деформации не возникают. За пределом упругости в теле возникают остаточные деформации и график, описывающий возвращение тела в первоначальное состояние после прекращения действия силы, изобразится не кривой ВО, а параллельной ей - CF. Напряжение, при котором появляется заметная остаточная деформация (»0,2 %), называется пределом текучести(s_т) - точка С на кривой. В области CD деформация возрастает без увеличения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести(или об­ластью пластических деформаций).Материалы, для которых область текучести значительна, называются вязкими,для которых же она практически отсутствует хрупкими.При дальнейшем растяжении (за точку D) происходит разрушение тела. Максимальное напряжение, возникающее в теле до разрушения, называется пределом прочности(s_p).

Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рисунок 3).

Рисунок 3 – Деформация изгиба

При изгибе на выпуклой стороне тело подвергается растяжению, а на вогнутой - сжатию. Внутри изгибаемого тела находится слой, не испытывающий ни растяжения, ни сжатия, называемый нейтральным слоем. Около него при деформации возникают лишь ничтожно малые упругие силы. Слои балки испытывают тем большее напряжение, чем дальше они находятся от нейтрального слоя. На рисунке 3 показана деформация изгиба. Пунктирная линия - нейтральный слой, стрелками показаны силы, действующие в некотором сечении ab.

Для деформации изгиба стержня с круглыми поперечным сечением, имеющим две точки опоры, когда сила приложена в середине расстояния между опорами, расчеты дают следующее выражение:

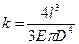, (4)

где k- коэффициент упругости при изгибе, пропорциональный приложенной силе,

l - расстояние между опорами;

D - диаметр стержня;

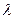- стрела прогиба (рисунок 3), .

Вычислив коэффициент упругости

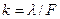, (5)

по (4) определим модуль Юнга:

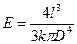. (6)

Описание экспериментальной установки

Внешний вид экспериментальной установки представлена на рисунке 4. Исследуемый стержень 1 свободно лежит на опорах 2. На середину стержня подвешиваются грузы 3. Над стержнем располагается микрометр со стрелочным отсчетным устройством 4 (индикаторная головка), который укреплен неподвижно на поперечной пластине 5, связанной с основой прибора.

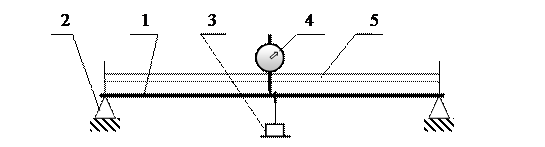
Рисунок 4 – Экспериментальная установка

Микрометр - универсальный инструмент, предназначенный для измерений с высокой точностью в области малых размеров. Действие микрометра основано на перемещении винта вдоль оси при вращении его в неподвижной гайке.

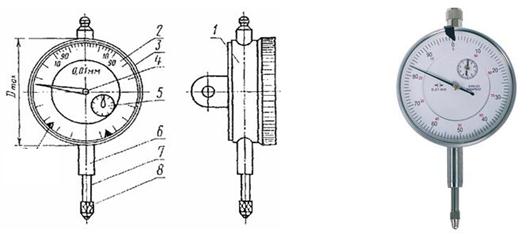
1 - корпус; 2 - циферблат; 3 - ободок; 4 - стрелка; 5 – указатель числа оборотов; 6 - гильза;

7 - измерительный стержень; 8 – измерительный наконечник

Рисунок 5 – Индикаторная головка

Микрометр со стрелочным отсчетным устройством (индикаторная измерительная головка) представлен на рисунке 5. Циферблат 2 имеет две шкалы (черные и красные цифры). Отсчет показаний производят по внешней (черной) шкале, если стрелка отклоняется вправо от нуля, причем отклонение берется со знаком плюс. Отсчет показаний при отклонении стрелки влево производят по внутренней (красной) шкале и берут со знаком минус. Перемещение измерительного стержня на целое число миллиметров приводит к полному обороту стрелки 4 и отсчитывается стрелкой указателя оборотов по малой шкале 5. Например, на фотографии (рисунок 5) показания прибора составляют 0,83 мм.

С помощью микрометра будем измерять прогиб стержня при его нагружении. Прежде всего, необходимо определить показания микрометра в отсутствии нагрузки. Это значение примем за нулевое. При нагружении стержня показания микрометра будут меняться. Отклонение показаний от нулевого значения и есть 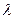- стрела прогиба (рисунок 3).

Значение действующей силы определяется исходя из массы груза

, (7)

где g – ускорение свободного падения.

Чем больше действующая на стержень сила, тем больше должен быть его прогиб. Если деформация стержня подчиняется закону Гука, то зависимость 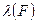должна быть линейной (рисунок 6). Таким образом, если по экспериментальным значениям удается построить график функции в виде прямой наклонной линии, проходящей через начало координат, то можно говорить о соблюдении закона Гука.

Рисунок 6 – Зависимость прогиба стержня от действующей силы

Обратите внимание, что экспериментальные точки вследствие влияния погрешностей измерений могут и не лежать на одной прямой. Поэтому следует провести такую усредненную прямую линию, для которой отклонения точек в обе стороны будут приблизительно одинаковыми.