Методы расчета показателей оптимальных партий заказа при многономенклатурных поставках: теоретический аспект

При наличии па складе поставщика широкой номенклатуры продукции (товаров) встает вопрос о возможной организации одновременной поставке потребителю и номенклатур. Аргументами в пользу объединения разных номенклатур в один заказ являются:

- требование поставщика о стоимости каждого заказа не ниже некоторой предельной величины;

- реализация полной загрузки используемых транспортных средств;

- ограничение количества отправок и их периодичности каждому клиенту (синхронизация поставок);

- снижение затрат на организацию, комплектацию партий поставок, поставляемых клиенту.[1, c.135]

Рассмотрим составляющую затрат, связанную с многономенклатурной поставкой от одного поставщика. Очевидно, эти затраты можно представить в виде двух составляющих: постоянной С₀ (определяемой главным образом стоимостью транспортировки) и переменной Сi, зависимой от объема выполняемых на складе операций при формировании заказа. Тогда для каждой i-й номенклатуры затраты, связанные с организацией одном поставки, будут определяться по формуле (2.1):

(2.1)

а для всей номенклатуры в виде одной поставки по формуле (2.2):

При независимых заказах для каждой i-й позиции номенклатуры расчет оптимальной величины заказа S_0i, количества заказов периодичности и минимальных суммарных затрат производится по основным формулам модели EOQ. При подстановке вместо С₀ суммирование по всей номенклатуре позволяет получить оценку затрат при независимой поставке каждой i-й позиции (2.3):

При одновременной поставке n позиций номенклатуры ее периодичность Т будет отличаться от оптимальных периодичностей независимых поставок для каждой из компонент.[1, c.136]

Рассмотрим один из возможных подходов к решению задачи. Запишем основное уравнение для суммарных затрат i-й номенклатуры в виде (2.4):

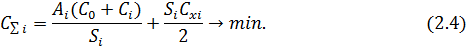
Известно, что размер i-й поставки можно определить по формуле (2.5):

При подстановке (2.5) в формулу (2.4) получим (2.6):

Очевидно, что при условии = T, т. е. одновременной поставки n позиций номенклатуры, уравнение для суммарных затрат можно представить в виде (2.7):

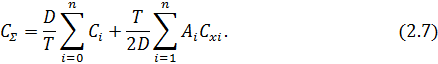
Определим оптимальное значение периодичности многономенклатурной поставки , воспользовавшись стандартной процедурой, т. е. возьмем производную по Т и приравняем ее нулю, получим (2.8):

Из уравнения (2.8) находим выражение для оптимальной периодичности:

Найдем остальные показатели, характеризующие многономенклатурную поставку:

- размер i-й поставки (2.10):

- количество поставок (2.11):

При подстановке в формулу (2.7) после преобразований находим выражение для минимальных суммарных затрат (2.12):

При расчете многономенклатурных поставок особое значение приобретает учет ограничений, связанных с объемом (площадью) и грузоподъемностью транспортных средств, объемом (площадью) складских помещений, наличием средств для приобретения всей партии и т. д.[1, c.137]

Проведенные расчеты показали, что в общем виде учет ограничений указанных параметров производится с использованием формулы (2.13):

где G_v - предельные значения физического или экономического показателя;

- интенсивность потребления (расхода) i-го продукта, ед./день;

- физический или экономический показатель i-го продукта.

Для вывода формулы (2.13) запишем уравнение (2.14), учитывающее ограничение на один из возможных параметров, входящих в уравнение суммарных затрат, например, грузоподъемность транспортного средства (контейнер, кузов автомобиля, вагон и т.п.)

где - вес i-й единицы продукции, входящий в многономенклат.запас;

G - грузоподъемность транспортного средства;

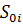- величина оптимальной партии при независимой поставке.

Для расчета многономенклатурного заказа с учетом ограничения (2.14) воспользуемся методом множителей Лагранжа. Поскольку и связаны зависимостью (2.10), то функция Лагранжа может быть записана в виде (2.15):

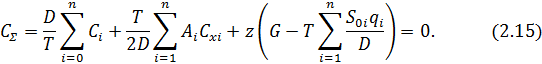
Далее до конца параграфа для упрощения формулы не будем указывать индексы i и n при записи сумм, подразумевая, что , и т. д.[1, c.138]

Для определения оптимальных значений Т и z возьмем частные производные и и приравняем их нулю, получим (2.16):

Из первого уравнения системы (2.16) находим (2.17):

Запишем ограничение (2.14) в виде (2.18):

При подстановке в последнее уравнение выражения для Т
(формула (2.17)), получим (2.19 a,b,c):

т.е.

или

Таким образом, множитель Лагранжа равен (2.20):

При подстановке z в формулу (2.17) для Т находим (2.21):

Нетрудно заметить, что полученная зависимость (2.21) идентична ограничению (2.14), ввиду соотношения (2.22):

что и требовалось доказать.

Таким образом, для многономенклатурной поставки учет ограничений сводится к выполнению следующего правила:

- если период многономенклатурной поставки , то ее показатели рассчитываются по формулам (2.9)-(2.12);

- если 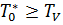, то в качестве расчетного периода принимается и производится корректировка , и ( ) по формулам (2.23)-(2.25):

При наличии нескольких критериев для выбора наилучшего варианта можно воспользоваться следующим правилом (2.26):

где - периоды времени, рассчитанные по формуле (2.13) с учетом различных критериев: объем, вес, затраты и т. п.[1, c.140]