КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПРИЛОЖЕНИЕ. 1. Решить уравнение методом половинного деления, хорд с точностью .
1. Решить уравнение методом половинного деления, хорд с точностью 
.
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
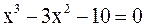
2. Решить уравнение методом Ньютона и итерации с точностью .
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
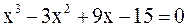
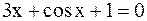
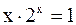
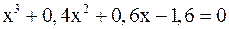
3. Решить уравнение методом хорд и касательных и видоизменённым Ньютона с точностью .
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
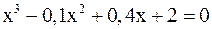
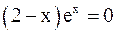
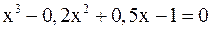
4. Решить систему 
методом простой итерации с точностью .
| С | d | С | d | ||
| 
| 
|
| ||
|
| 
| 
| ||
|
| 
| 
| ||
|
| 
|
| ||
|
| 
| 
| ||
| 
| 
|
| ||
| 
| 
|
|
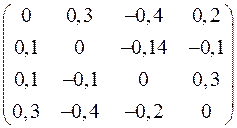
5. Решить систему 
методом Зейделя с точностью .
| А | b | A | b | ||
| 
| 
| 
| ||
|
| 
| 
| ||
| 
| 
|
| ||
|
| 
|
| ||
| 
| 
| 
| ||
|
| 
| 
| ||
| 
| 
| 
|
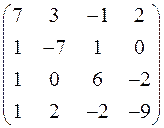
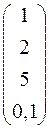
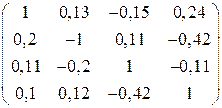
6. Решить систему методом простой итерации с точностью .
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
7. Решить систему методом Ньютона с точностью .
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
|
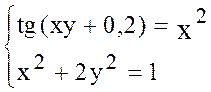
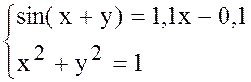
8. По заданным значениям 
и 
найти прямую 
и параболу 
методом наименьших квадратов. Найти погрешность. Построить прямую и кривую в той же системе координат, где нанесены данные точки.
 |
 |
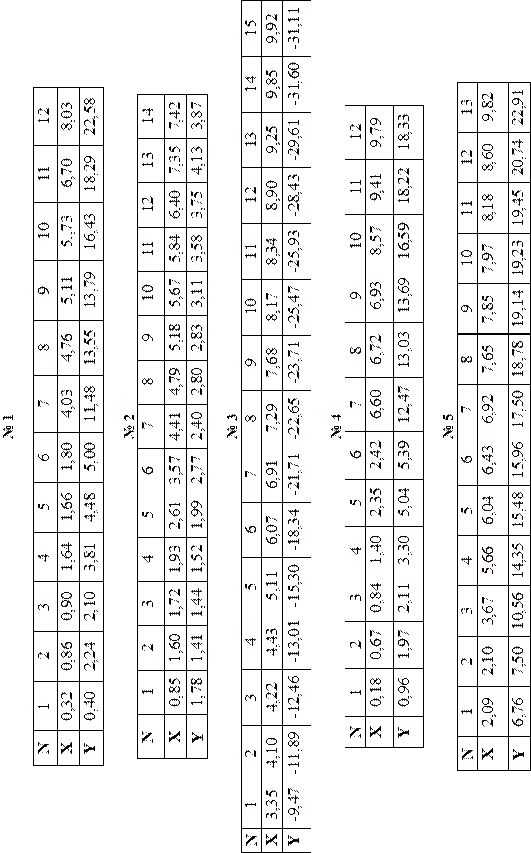
9. 1) Заданы значения функции
в узлах 
, получающиеся делением отрезка 
на 5 частей. Найти значения функции при 
и 
с помощью интерполяционных формул Ньютона.
|
| ||||||||||||||
| 0,1 | 1,0 | 1,1 | 0,9 | 0,9 | 0,8 | 1,1 | 1,0 | 1,2 | 1,2 | 1,1 | 0,8 | 0,8 | 0,8 | 1,1 |
| 1,2 | 2,1 | 2,2 | 2,0 | 1,9 | 2,0 | 2,2 | 2,1 | 1,8 | 2,0 | 1,9 | 2,0 | 2,2 | 1,8 | 2,2 |
| 1,4 | 2,9 | 3,2 | 3,0 | 3,2 | 2,9 | 3,2 | 3,1 | 3,2 | 3,0 | 3,2 | 2,8 | 2,9 | 2,9 | 3,0 |
| 1,6 | 3,8 | 4,2 | 3,8 | 3,8 | 4,2 | 4,2 | 3,8 | 4,1 | 3,8 | 3,8 | 4,0 | 4,0 | 4,0 | 4,1 |
| 1,8 | 5,2 | 5,2 | 5,1 | 5,1 | 5,2 | 5,1 | 5,2 | 5,2 | 5,0 | 4,9 | 5,2 | 5,2 | 4,9 | 4,9 |
| 2,0 | 5,9 | 6,0 | 5,8 | 6,1 | 5,8 | 5,9 | 6,2 | 6,1 | 6,1 | 5,8 | 6,0 | 5,8 | 6,1 | 5,9 |
2) Заданы значения 
функции в точках . Найти значение функции при 
. Задачу решить с помощью интерполяционного многочлена Лагранжа.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 
| 
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. Решить краевую задачу методом прогонки.
| № | Дифференциальное уравнение | Краевые условия | 
| 
|
| 
| 
| ||
| 
|
| ||
| 
| 
| ||
| 
|
| ||
| 
|
| ||
| 
| 
| ||
| 
|
| ||
| 
|
| ||
| 
|
| ||
| 
|
| ||
| 
| 
| ||
| 
|
| ||
| 
|
| ||
| 
|
|
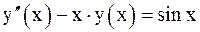
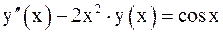
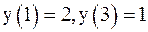
11. Решить задачу Коши методом Эйлера и Рунге – Кутта.
| № | Дифференциальное уравнение | Начальное условие | 
|
|
| 
| 
| ||
| 
|
| ||
| 
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
| 
| ||
|
|
| ||
|
|
| ||
|
|
|
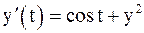
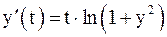
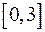
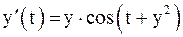
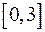
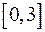
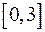
12. Решить системы нелинейных уравнений методом скорейшего спуска.
| № | ||
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
|
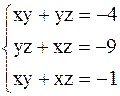
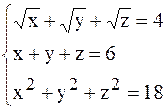
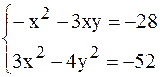
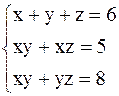
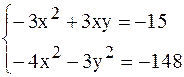
13. Решить задачу Коши модифицированными методами Эйлера.
| № | Дифференциальное уравнение | Начальное условие |
| № |
| 
| 
| ||
| 
|
| ||
|
|
| ||
| 
|
| ||
| 
| 
| ||
| 
|
| ||
| 
|
| ||
|
|
| ||
|
|
| ||
| 
| 
| ||
| 
|
| ||
| 
|
| ||
|
|
| ||
|
|
|
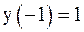
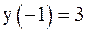
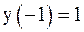
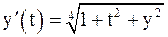
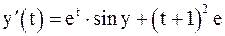
14. Найти собственные значения матрицы: 
.
 = 3;
|  = 7;
| = 6;
| = 7;
| ||
| = 5;
| = 3;
| = 6;
| = -7;
| ||
| = 3;
| = 8;
| = 7;
| = -5;
| ||
| = -3;
| = 5;
| = 5;
| = 9;
| ||
| = 7;
| = 6;
| = 9;
| = 3;
| ||
| = -3;
| = -5;
| = 8;
| = 5;
| ||
| = 5;
| = -8;
| = -6;
| = -8.
|
15. Вычислить определённый интеграл с точностью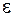 
методом Симпсона.
| № | интеграл |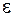
| № | интеграл |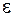
|
| 0,001 | 
| 0,0001 | ||
| 0,0001 | 
| 0,01 | ||
| 0,01 | 
| 0,001 | ||
| 0,001 | 
| 0,01 | ||
| 0,0001 | 
| 0,0001 | ||
| 0,01 | 
| 0,01 | ||
| 0,001 | 
| 0,0001 |
Дата добавления: 2015-01-05; просмотров: 89; Мы поможем в написании вашей работы!; Нарушение авторских прав |