
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Двукратно интегрирующие системы.
Когда необходимо поддерживать скорость с высокой точностью и свести к 0 установившуюся ошибку, применяют ПИ регулятор с передаточной функцией:

где  ,
,  ,
,  .
.

Параметры регулятора скорости чаще всего выбираем из условий настройки на СО в соответствии:
 ,
,  ,
,  ,
, 
 Передаточная функция разомкнутого и замкнутого контуров:
Передаточная функция разомкнутого и замкнутого контуров: 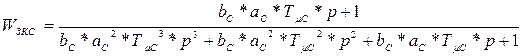
Подставив в выражении передаточной функции: (**)
 ,
, 
Из последней формулы (**) следует, что в установившемся режиме отклонения равны 0. В двукратно интегрирующей системе характер п.п. определяется 2-мя параметрами:
1)коэффициентом пропорциональности Kрс(ас)
2) Постоянной интегрирующей скорости Тис(bc).
При ступенчатом изменении М при настройке на СО скорость изменяется:
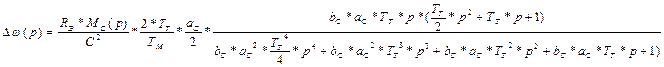

 (***)
(***)
 1)
1)  2)
2)  ,
, 
Процесс изменения отклонения скорости для данного случая имеет кривая (1). Максимальное динамическое отклонение wсоставляет около 0.9, т.е. такое же, как в однократно интегрирующей системе, настроенной на МО(  ).
).
 При высоких значениях коэффициентов пропорциональности усиления
При высоких значениях коэффициентов пропорциональности усиления  и малой постоянной времени интегрирования
и малой постоянной времени интегрирования 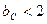 выражение (**) для отклонения w при ударном применении нагрузки должно быть заменено точными, учитывающими член 2-го порядка в характеристическом уравнении контура тока. При
выражение (**) для отклонения w при ударном применении нагрузки должно быть заменено точными, учитывающими член 2-го порядка в характеристическом уравнении контура тока. При  это выражение (***).
это выражение (***).
С увеличением Kрс(ас<2) происходит уменьшение динамического падения w, но одновременно увеличивается колебательность системы,=> применение ПИ-регулятора скорости позволяет свести к нулю установившуюся ошибку, но в то же время не даёт возможности существенно уменьшить динамического падения w.
Дата добавления: 2015-01-14; просмотров: 363; Мы поможем в написании вашей работы!; Нарушение авторских прав |