
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Однократноинтегрирующая система АЭП
Структурная схема контура скорости представлена на рисунке 5.26.
DIс = 0.
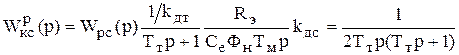 ;
;
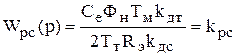 .
.
С этим П-регулятором система астатична по заданию и статична по возмущению. В целом система статическая.
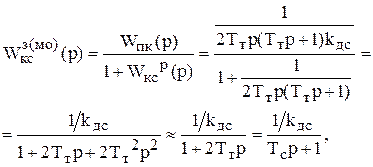
где Тс = 2Тт – эквивалентная постоянная времени оптимизированного на МО контура скорости.
 .
.
УР: 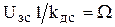 .
.
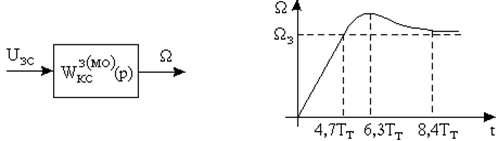 Рисунок 5.27
Рисунок 5.27
|
График переходного процесса контура скорости представлен на рисунке 5.27. Такой характер переходного процесса будет в том случае, если все звенья системы являются линейными (не выходят на ограничение регулятора скорости). С данным регулятором контур скорости является астатическим первого порядка по заданию.
При подаче линейного сигнала задания появляется ошибка по скорости, т.е. система является статической по заданию. Порядок астатизма равен номеру производной во входном сигнале, при котором контур становится статическим, т.е. появляется ошибка по скорости.
Передаточная функция контура скорости по возмущению


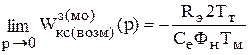 ;
;
УР: 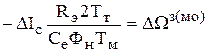 .
.
По возмущению контур скорости является статическим. Величина ошибки пропорциональна Iс.
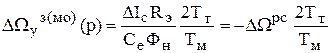 ;
;
В некоторых случаях получается 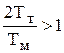 .
.
Типовые СУЭП с подчиненным регулированием координат
Широкое применение на практике унифицированных блочных систем управления электроприводом с последовательной коррекцией позволяет достичь оптимальных показателей качества переходных процессов, широкой унификации схем и конструкций элементов, удобства и простоты наладки регуляторов, легкость решения задач ограничения регулируемых величин, сокращение времени пуска автоматизируемых объектов.
Система подчиненного регулирования строится в соответствии с обобщенной структурной схемой, приведенной на рисунке 4.25. Она образуется из нескольких контуров регулирования, число которых равно числу регулируемых параметров. В каждом контуре имеется выходное звено, или собственно объект регулирования 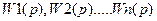 и регулятор
и регулятор  .
.
Контуры регулирования соединяются последовательно, образуя взаимосвязанную многоконтурную систему. На входе каждого регулятора сравниваются два воздействия: задающие Xij, регулируемой величины, и сигнал обратной связи Xoc.i пропорциональный действительному значению этой величины.
Отдельные контура соединяются таким образом, что выходное напряжение регулятора i-го контура регулирования служит задающим напряжением для (i-1)
 |
контура, являющеюся внутренним по отношению к i-ому контуру.
Входной сигнал регулирования первого самого внутреннего контура XP1 служит для выработки регулирующего воздействия на объект регулирования этого контура W1(Р).
При таком соединений внутренние контуры оказываются подчиненными внешним контурам регулирования. При этом объект регулирования Wоi(Р) какого либо i-го контура оказывается состоящим из выходного звена данного контура W1(Р), т. е. собственно объекта, и замкнутого (i-1)-го контура регулирования, внутреннего по отношению к данному контуру.
Учитывая обозначения на рисунке 4.25 передаточная функция объекта регулирования, (например второго контура) Wо2(Р) имеет вид:
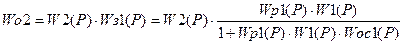 ,
,
где W2(Р) - передаточная функция собственного объекта;
W01 (Р) = W1(Р) - передаточная функция объекта первого контура;
Wр1(Р) - передаточная функция регулятора первого контура;
Wз1(Р) - передаточная функция замкнутого первого контура;
Wос(Р) - передаточная функция цепи обратной связи.
(В целях более компактной записи уравнений в дальнейшем в ряде случаев будем принимать Wос(Р)=1; Xвых.i=Xос.i).
Для самого внутреннего контура, первого, передаточная функция объекта регулирования W01(Р) совпадает с передаточной функцией W1(Р) собственно объекта.
В общем случае для передаточной функции объекта i-го контура
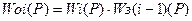 ,
,
где Wз(i-1) – передаточная функция замкнутого (i-1) контура.
Главным в системе является параметр самого внешнего контура регулирования, т.к. он определяет основную цель автоматического регулирования. Остальные параметры вспомогательные и подчинены главному. Кроме того, вспомогательные параметры также находятся в подчинении один с другим.
Расчет параметров и настройка систем подчиненного регулирования производится путем последовательной оптимизации отдельных контуров, начиная с самого внутреннего (i=1) до самого внешнего (i=n).
Под оптимизацией контура понимают выбор типа регулятора и настройку параметров последнего т.о., что бы наилучшим образом удовлетворялись технические требования с учетом ограничений в электрической и механической частях привода (перегрузочная способность двигателей, их нагрев, допустимая по условиям коммутации на коллекторе скорость нарастания тока, величины ускорений и ударов допустимых конструкцией механизмов и т.п.).
Способ подчиненного регулирования позволяет легко осуществить ограничения любого параметра, а также относительно просто рассчитать и настроить систему так, чтобы она удовлетворяла поставленным требованиям.
Для ограничения какого-либо параметра хi достаточно ограничить выходную величину регулятора (i+1)-го контура, что на практике не представляет затруднений. До тех пор, пока (i+1)-й регулятор находится в состоянии насыщения, напряжение на его выходе остается постоянным. Цепь регулирования для (i+1)-го и всех внешних по отношению к нему контуров благодаря этому размыкается и регулируется только величина хi, заданное значение которой
 .
.
при этом остается постоянным. Когда при увеличении параметра Х(i+1) выходное напряжение (i+1)-го регулятора окажется меньше предельного значения, последний выйдет из режима насыщения и начнет регулировать X(i+1) параметр, работая на линейной части своей характеристики. Если ни один из регуляторов не работает в зоне насыщения, осуществляется регулирование всех параметров системы. Таким образом, структура подчиненного регулирования, в принципе, обеспечивает возможность настройки каждого внутреннего контура независимо от настройки его внешних контуров. Благодаря этому в такой структуре возможно введение в контур регулирования параметров дополнительных формирующих и корректирующих устройств, необходимых для получения требуемого качества регулирования этой величины, так что эти устройства не оказывают влияния на качество работы всех контуров регулирования, внутренних по отношению к данному.
Выбор регуляторов в системе подчиненного регулирования производится, как правило, исходя из требований достижения минимального времени отработки управляющих воздействий при заданном качестве переходного процесса во всех контурах регулирования.
(58),(74),(47) Оптимум по модулю (технический)
Для достижения предельного быстродействия в идеальном случае требуется, чтобы каждый разомкнутый контур был безинерционным, и его передаточная функция совпадала с коэффициентом передачи.
Передаточная функция объекта какого-либо контура регулирования Wо1(Р) может быть представлена в виде:
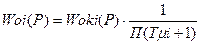 , (4.67)
, (4.67)
где Woki(Р) - передаточная функция части объекта, содержащая значительные инерционности, действие которых компенсируется действием регулятора.
Tμi - "малые постоянные времени", действие которых не компенсируется. К "малым" относятся постоянные времени, сопрягающие частоты которых  (
( 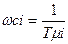 ) значительно превосходят частоту среза системы
) значительно превосходят частоту среза системы  :
:
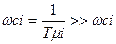 . (4.68)
. (4.68)
"Малыми" постоянными времени являются: постоянные времени фильтров тахогенераторов, датчиков тока, быстродействующих СИФУ, электронных усилителей и т.п.
Если условие (4.68) удовлетворяется, то для практических расчетов действие нескольких последовательно соединенных апериодических звеньев с малыми постоянными времени 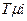 может быть заменено действием одного апериодического звена с постоянной времени
может быть заменено действием одного апериодического звена с постоянной времени  равной сумме постоянных времени отдельных звеньев:
равной сумме постоянных времени отдельных звеньев:
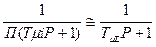 , (4.69)
, (4.69)
где 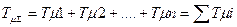 , а передаточная функция (4.67) имеет вид:
, а передаточная функция (4.67) имеет вид:
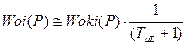 . (4.70)
. (4.70)
При применении последовательной коррекции исходят из того, что компенсаций подлежат лишь большие и средние инерционности объекта. В контур регулирования желательно вводить интегрирующий элемент (он не реагирует на помехи), который обеспечивает астатическое регулирование (статическая ошибка равна нулю). В соответствии с этим выбирают регулятор с передаточной функцией 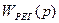 :
:
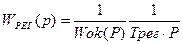 . (4.71)
. (4.71)
Передаточные функции системы регулирования в разомкнутом 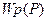 и замкнутом
и замкнутом  состояниях выражаются уравнениями:
состояниях выражаются уравнениями:
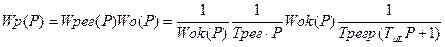 . (4.72)
. (4.72)
В замкнутом состоянии:
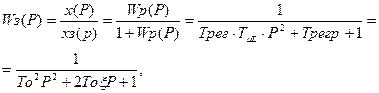 (4.73)
(4.73)
где 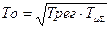 ; (4.74)
; (4.74)
 - коэффициент затухания (демпфирования). (4.75)
- коэффициент затухания (демпфирования). (4.75)
Из (4.73) видно, что система второго порядка устойчива. Переходные процессы в системе при отработке задающего воздействия не зависят ни от коэффициента усиления, ни от больших инерционностей объекта, которые скомпенсированы, а зависят только от нескомпенсированных малых постоянных времени объекта регулирования  от постоянной времени интегрирования регулятора Трег.
от постоянной времени интегрирования регулятора Трег.
Эта настройка с компенсацией больших постоянных времени. Продолжительность и характер переходных процессов определяются величиной и соотношением постоянных времени регулятора Трег и нескомпенсированных малых постоянных времени объекта  .
.
В установившемся режиме (Р=0) 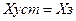 .
.
Продолжительность и характер переходного процесса при изменении задающего воздействия при заданной величине нескомпенсированных малых постоянных времени объекта  определяется величиной постоянной времени интегрирования регулятора Трег т.к. от их отношения
определяется величиной постоянной времени интегрирования регулятора Трег т.к. от их отношения
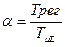 (4.76)
(4.76)
зависят коэффициент затухания 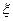 и собственная частота незатухающих колебаний
и собственная частота незатухающих колебаний 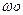 :
:
 . (4.77)
. (4.77)
При нулевых начальных условиях и скачкообразном изменении задающего воздействия получим (на основании 4.73) выражение переходной функции:
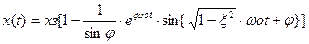 , (4.78)
, (4.78)
где 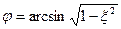 .
.
При малой Трег, а<<1, и 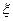 <<1,
<<1, 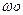 велико. Процесс сопровождается большим перерегулированием и длительными колебаниями (кривая 1 на рис. 4.26). При большей Трег:
велико. Процесс сопровождается большим перерегулированием и длительными колебаниями (кривая 1 на рис. 4.26). При большей Трег:
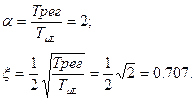 (4.79)
(4.79)
 |
а) графики переходных процессов;
б) логарифмическая характеристика
Рисунок 4.26 – Графики переходных процессов и ЛАХ
На рисунке 4.26:
1- 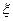 =0,25 (а=0,25) 2-
=0,25 (а=0,25) 2- 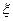 =0,707 (а=2) 3-
=0,707 (а=2) 3- 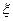 =1 (а=4) 4-
=1 (а=4) 4- 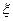 =1.2 (а>4)
=1.2 (а>4)
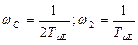
Характер переходного процесса показан на рисунке 4.26. Выходная величина в первый раз достигает заданного значения 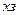 , через время Тр2 =4.7·
, через время Тр2 =4.7·  а перерегулирование окажется равным:
а перерегулирование окажется равным:
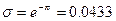 ,
,
или всего 4.33%. Максимального значения регулирования величина σ достигает через время Тmах = 2· 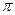
 (кривая 2, рис. 4.26, а).
(кривая 2, рис. 4.26, а).
Для большинства практических применений процесс регулирования считается законченным, если регулируемая величина отклоняется от заданного значения не более, чем на 5%.
При настройке регулятора по условию 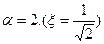 регулируемая величина достигает значения 0.95
регулируемая величина достигает значения 0.95 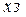 через время tр1=4.1
через время tр1=4.1  , и в дальнейшем отклонение ее от заданного значения никогда не превысит 5%.
, и в дальнейшем отклонение ее от заданного значения никогда не превысит 5%.
Если взять регулятор с еще меньшим быстродействием (a=4; 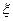 =1), то переходной процесс приобретает монотонный апериодический характер без перерегулирований (кривая 3 рисунок 4.26, а). Снижение скорости регулирования при апериодическом характере переходных процессов в большинстве случаев нежелательно. В связи с этим наиболее часто применяют настройку регулятора из условия
=1), то переходной процесс приобретает монотонный апериодический характер без перерегулирований (кривая 3 рисунок 4.26, а). Снижение скорости регулирования при апериодическом характере переходных процессов в большинстве случаев нежелательно. В связи с этим наиболее часто применяют настройку регулятора из условия 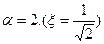 и называют ее настройкой на оптимум по модулю ОМ (технический). Эта настройка является известным компромиссом между быстродействием и величиной перерегулирования. Она не является оптимальной по быстродействию и по перерегулированию; однако в большинстве случаев она удовлетворяет и тому и другому.
и называют ее настройкой на оптимум по модулю ОМ (технический). Эта настройка является известным компромиссом между быстродействием и величиной перерегулирования. Она не является оптимальной по быстродействию и по перерегулированию; однако в большинстве случаев она удовлетворяет и тому и другому.
Можно показать, что его условие отвечает требованию максимального приближения модуля частотной характеристики 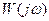 к единице в возможно более широкой полосе частот, чем и объясняется термин оптимум по "модулю". Асимптотическая ЛАЧХ разомкнутой системы с передаточной функцией (4.72) приведена на рисунке 4.26, б.
к единице в возможно более широкой полосе частот, чем и объясняется термин оптимум по "модулю". Асимптотическая ЛАЧХ разомкнутой системы с передаточной функцией (4.72) приведена на рисунке 4.26, б.
Соответствующий запас по фазе:

Из теории автоматического управления известно, что динамические свойства подобных систем для многих практических случаев благоприятны.
Такое выполнение регуляторов обеспечивает за счет форсировки процесса компенсацию больших инерционностей объекта и при настройке на ОМ (а=2) превращает систему в колебательное звено с малым колебанием и достаточно высоким быстродействием.
Общие правила выбора регулятора и оптимальной настройки контура методом компенсации основных инерционностей объекта регулирования (согласно 4.71):
1. Каждому звену с большой постоянной времени в объекте регулирования должно соответствовать звено с обратной передаточной функцией и с такой же постоянной времени в составе регулятора.
2. Постоянная интегрирования регулятора Трег выбирается из условия:
Трег = 2 
Поведение замкнутого оптимизированного контура при задающем воздействии определяется лишь суммой малых постоянных времени  . После оптимизации первого внутреннего контура регулирования производится оптимизация второго контура.
. После оптимизации первого внутреннего контура регулирования производится оптимизация второго контура.
Таким образом, при настройке контуров регулирования на ОМ передаточная функция внутреннего замкнутого контура при рассмотрении работы внешнего контура может быть приближенно представлена в виде эквивалентного апериодического звена с малой постоянной времени Трег = а· 
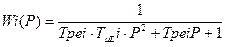
 . (4.80)
. (4.80)
При подобном допущении объект регулирования второго контура представляется состоящим из собственного объекта второго контура и апериодического звена с "малой" постоянной времени 
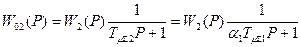 . (4.81)
. (4.81)
При этом роль звена с малой некомпенсируемой постоянной времени выполняет оптимизированный внутренний контур.
При настройке регуляторов по условию оптимума по модулю (а=2 или 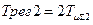 ) передаточная функция разомкнутого внешнего (второго) контура имеет вид:
) передаточная функция разомкнутого внешнего (второго) контура имеет вид:
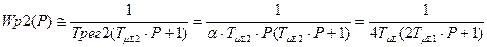 (4.82)
(4.82)
соответствует выражению для внутреннего контура с тем различием, что процесс протекает вдвое дольше.
(48 ) Симметричный оптимум
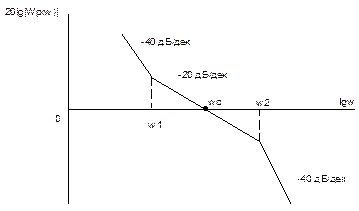 |
В определенных ситуациях система управления должна удовлетворять отличным от условий ОМ требованиям уменьшения динамических ошибок, астатизма по отношению не только к задающему, но и возмущающему воздействиям и повышенного быстродействия при больших значениях допустимого пере регулирования. Эти свойства могут быть обеспечены за счет больших коэффициентов усиления в низкочастотной области ЛАЧХ разомкнутого контура, чем при ОМ в этой области, участком с наклоном - 40 дБ/дек. Переход к этому участку, симметричный по сопрягающей частоте 1/4
 перехода к высокочастотной асимптоте - 40 дБ/дек относительно частоты среза
перехода к высокочастотной асимптоте - 40 дБ/дек относительно частоты среза 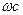 = 1/2
= 1/2  (рисунок 4.27) приводит к ЛАЧХ отвечающей, так называемому условию "симметричного оптимума" (СО) для переходного процесса в замкнутом контуре. Таким образом ЛАЧХ, соответствующие ОМ и СО отличаются только наклоном при
(рисунок 4.27) приводит к ЛАЧХ отвечающей, так называемому условию "симметричного оптимума" (СО) для переходного процесса в замкнутом контуре. Таким образом ЛАЧХ, соответствующие ОМ и СО отличаются только наклоном при 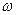 < 1/4
< 1/4  , равным - 20 дБ/дек при ОМ и - 40 дБ/дек при СО.
, равным - 20 дБ/дек при ОМ и - 40 дБ/дек при СО.
Рисунок 4.27
 |
Рисунок 4.28
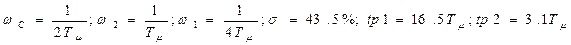
Соответствующий запас по фазе составляет для СО примерно 40 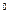 что приводит к большим пере регулированиям при переходных процессах. Непосредственно по виду ЛАЧХ (рисунок 4.27.) легко установить, что желаемая передаточная функция разомкнутого контура, отвечающая условиям СО, принимает следующий вид:
что приводит к большим пере регулированиям при переходных процессах. Непосредственно по виду ЛАЧХ (рисунок 4.27.) легко установить, что желаемая передаточная функция разомкнутого контура, отвечающая условиям СО, принимает следующий вид:
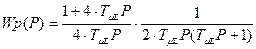 . (4.83)
. (4.83)
Эта передаточная функция отличается от аналогичной при настройке на ОМ только первым сомножителем, увеличивающим порядок астатизма системы. Для замкнутого контура имеет отсюда передаточную функцию
 (4.84)
(4.84)
и переходную характеристику
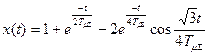 . (4.85)
. (4.85)
Анализ переходного процесса, описываемого выражением (4.83) показывает, что пере регулирование при СО составляет  время первого перехода через установившееся значение равно
время первого перехода через установившееся значение равно 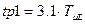 и время выхода в зону отклонений от этого значения не превышающее 2%, составляет
и время выхода в зону отклонений от этого значения не превышающее 2%, составляет  (рисунок 4.28). При настройке на ОМ -
(рисунок 4.28). При настройке на ОМ - 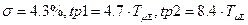 .
.
Значительное перерегулирование обусловлено здесь форсирующим звеном в числителе выражения (4.84), а не корнями характеристического полинома. Если оно не желательно, то его можно снизить, включая апериодический фильтр на входе системы и не изменяя при этом свойств контура относительно, например, возмущающего воздействия. При настройке на СО регулятор всегда содержит интегрирующее звено и система является астатической, отрабатывающей без ошибки как управляющие, так и возмущающие воздействия.
Настройки на ОМ и СО не являются ни оптимальными, ни универсальными для всех случаев. В зависимости от структуры объекта регулирования, соотношения постоянных времени отдельных элементов, требований технологического процесса и других факторов могут применяться различные типы регуляторов и другие настройки.
Наилучший вариант настройки контура определяется соотношением
постоянных времени Трег и  . Анализируя динамику контура при возмущающем воздействии при указанных настройках (ОМ; СО) следует, что при
. Анализируя динамику контура при возмущающем воздействии при указанных настройках (ОМ; СО) следует, что при
То = (2.5 - 3)· 4  переходной процесс при настройке на СО будет лучше. Если
переходной процесс при настройке на СО будет лучше. Если
То > (2.5-3)·4  настройку следует вести на СО, т.к. идет более быстрая отработка возмущающих воздействий. Настойка на ОМ обеспечивает более стабильную динамику электропривода в условиях влияния помех, пульсаций переменных величин и довольно широкого изменения параметров системы регулирования.
настройку следует вести на СО, т.к. идет более быстрая отработка возмущающих воздействий. Настойка на ОМ обеспечивает более стабильную динамику электропривода в условиях влияния помех, пульсаций переменных величин и довольно широкого изменения параметров системы регулирования.
Рассмотренные критерии базируются, в основном, на удобстве технической реализации настройки.
(49) Контур регулирования тока
Рассмотрим наиболее распространенную схему управления вентильным электроприводом постоянного тока с обратной связью по скорости с двухконтурной системой подчиненного регулирований тока и скорости приведенную на рисунке 4.29. В данной схеме двигатель постоянного тока М питается от тиристорного преобразователя U с системой импульсно-фазового управления СИФУ. Управляющее напряжение Uу поступает на СИФУ с выхода регулятора тока РТ(Uу = Uрт). На входе регулятора тока происходит сравнение
задающего напряжения Uзт и напряжения обратной связи по току Uост, получаемого с датчика тока ДТ. Задающим напряжением для регулятора тока РТ служит выходное напряжение регулятора скорости РС(Uзт =Uрc), т.е. контур регулирования тока подчинен контуру регулирования скорости. Задающее напряжение на вход регулятора скорости поступает либо непосредственно с командного органа или через сглаживающее устройство, например, с задатчика интенсивности ЗИ. Напряжение обратной связи по скорости Uосc- поступает либо от тахогенератора BR либо от датчика ЭДС (например, с тахометрического моста).
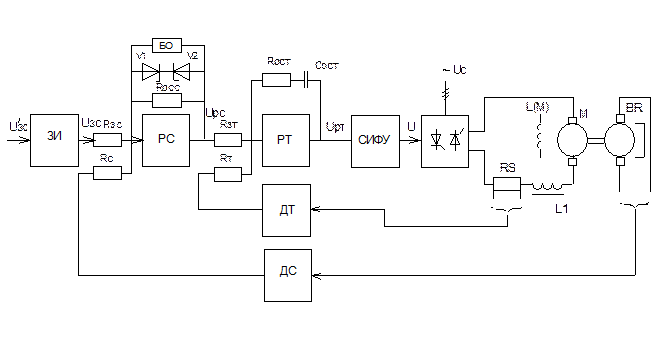
Рисунок 4.29 – Функциональная схема двухконтурной системы подчиненного регулирования
Для ограничения максимальной величины тока задающее напряжение регулятора тока Uзт ограничивается путем шунтирования регулятора скорости либо стабилитронами VI,V2, либо специальным источником опорного напряжения БО (рисунок 4.29).Если напряжение на выходе регулятора скорости меньше напряжения пробоя стабилитронов или опорного напряжения Uо, то регулятор скорости нормально работает в соответствии с его настройкой. Если же его выходное напряжение становится больше напряжения пробоя стабилитронов (или опорного напряжения), то сопротивление обратной связи усилителя становиться практически равным нулю, и дальнейший рост задающего Uзт напряжения невозможен.
На основе схемы управления (рисунок 4.29) составлена структурная схема, приведенная на рисунке 4.30.
В данной схеме, как и в большинстве других систем подчиненного регулирования электроприводами, контур тока является внутренним. С него начинают расчет и настройку многоконтурной системы. Оптимизированный токовый контур является составной частью объекта регулирования в системе управления скоростью. Результаты его настройки в значительной мере определяют быстродействие всей системы и качество регулирования.
Введение в систему управления электропривода отдельного регулятора тока позволяет решить следующие задачи:
1. Путём компенсации инерционности в силовой цепи за счёт действия регулятора тока формировать кривую тока якоря  таким образом, что бы обеспечивался, возможно, более быстрый рост тока при отсутствии перерегулирования.
таким образом, что бы обеспечивался, возможно, более быстрый рост тока при отсутствии перерегулирования.
2. Эффективно ограничивать (совместно с регулятором скорости) максимальные значения тока при перегрузках, т.к. контур тока является самым быстродействующим.
3. Эффективно ограничивать колебания тока и скорости при колебаниях напряжения питающей сети.
4. Обеспечивать равномерное распределение тока нагрузки при параллельной работе двух преобразователей на общую нагрузку и равномерное распределение нагрузки между двумя двигателями при жесткой связи их валов. Для этого достаточно лишь подавать задающее напряжение UЗТ на входе регуляторов тока обоих преобразователей от общего задатчика (с выхода общего регулятора скорости UЗТ = UРС ).
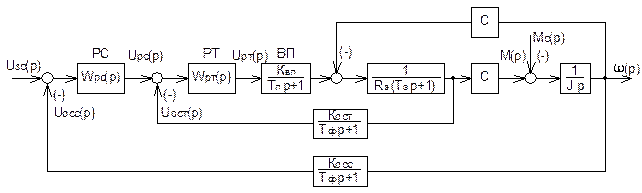
Рисунок 4.30 – Структурная схема двухконтурной системы подчиненного регулирования
Дата добавления: 2015-01-14; просмотров: 408; Мы поможем в написании вашей работы!; Нарушение авторских прав |