Электрическая цепь с распределенными параметрами (длинные линии). Дифференциальные уравнения длинной линии

В предыдущих главах рассматривались электрические цепи, которые называ­ют цепями с сосредоточенными параметрами.

При исследовании таких цепей считают, что электрическое поле сосредоточе­но в конденсаторах, эти участки были представлены на схемах с емкостями; маг­нитное поле сосредоточено в катушках индуктивности, в трансформаторах, эти участки на схемах обозначались индуктивностями; и, наконец, необратимые пре­образования электромагнитной энергии в тепловую, химическую и механическую были представлены на схемах с сопротивлениями.

В электротехнике, однако, часто встречаются электрические цепи, которые нельзя считать цепями с сосредоточенными параметрами.

Эти цепи называют цепями с распределенными параметрами, так как электри­ческое поле, магнитное поле и потери энергии распределены равномерно или не­равномерно вдоль всех участков цепи. В цепях с распределенными параметрами напряжения и токи различны не только на отдельных участках, но и изменяются в пределах каждого участка, т.е. зависят от пространственной координаты каждого участка. К цепям с распределенными параметрами относятся линии электропере­дач, линии телефонной и телеграфной связи, линии телеуправления и телеизмере­ния, антенны радиопередатчиков, обмотки трансформаторов и т.д.

За точку начала отсчета выберем начало линии.

Разность напряжений в начале и конце участка dx равна сумме падений на­пряжений на активном и индуктивном сопротивлениях.

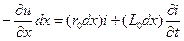
Изменение тока на участке равно сумме утечек тока через активную прово­димость и емкость, т.е.

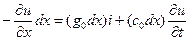
Частные производные в этих уравнениях записаны потому, что u(x,t) и i(x,t)- зависят от двух координат. Или

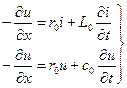телеграфные уравнения длинных линий.