Теорема Гаусса в интегральной и дифференциальной форме

Теорема Гаусса является одной из важнейших теорем электростатики. Она может быть сформулирована и записана тремя способами:

1. Поток вектора электрического смещения через любую замкнутую поверхность, окружающую некоторый объем, равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности

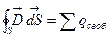
2. Так как , то теорема Гаусса для однородной и изотропной среды может быть записана в такой форме

3. Существует ещё одна форма записи теоремы Гаусса, отличающаяся от двух предыдущих

Дело в том, что поток вектора через любую замкнутую поверхность создается не только суммой свободных зарядов, но и связанных, находящихся внутри этой поверхности. Теорема Гаусса, записанная в интегральной форме, выражают связь между потоком вектора и алгебраической суммой зарядов, находящихся внутри этого объема. При помощи теоремы Гаусса в интегральной форме нельзя определить как связан источник линий в данной точке поля с плотностью свободных зарядов в той же точке поля. Ответ на этот вопрос даёт дифференциальная форма теоремы Гаусса.

1.

2.

3.