БИЛЕТ 16. Показатели безотказности невосстанавливаемых систем

В качестве случайной величины T примем наработку до отказа (единственного для систем данного класса). Считаем, что нам известна функция распределения F(t), которая в данном случае будет называться функцией вероятности отказа Q(t), т.е.:

.

Важнейшим количественным показателем безотказности служит функция вероятности безотказной работы в течение заданного времени t:

.

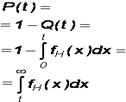Графики, дающие представление о характерах изменения функций P(t) и Q(t), представлены на рисунке:

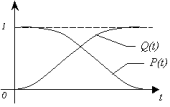
Плотность распределения вероятностей как показатель безотказности невосстанавливаемых систем принимает смысл плотности распределения наработки на отказ f_H(t), а интенсивность b(t) принимает смысл функции интенсивности отказов l(t):

.

.

Между функциями P(t) и l(t) существует взаимосвязь: .

Взаимосвязь между функциями f_H(t) и l(t) можно определить из соотношения:

.

Если одна из четырех функций известна, то остальные три можно вычислить по формулам, приведенным в таблице.

Удобный и наглядный физический смысл имеет показатель "средняя наработка на отказ", который равен математическому ожиданию времени исправной работы до первого отказа:

Свойства функции безотказной работы P(t):

1.При t=0, P(t)=1 , т.е. в нулевой момент времени система будет работоспособна.

2. P(t) — монотонно убывающая функция во времени.

3.При t→∞, P(t) → 0.

Определяемый показатель	Заданный показатель
Q(t)	P(t)	fn(t)	λ(t)
Вероятность отказа Q(t)	—	1 – P(t)
Вероятность безотказной работы P(t)	1 – Q(t)	—
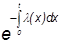
Плотность распределения наработки на отказ fn(t)			—
Интенсивность отказов l (t)				—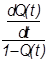

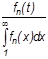
Экспериментальная оценка надежности, план испытаний.

Рассмотрим возможные планы испытаний:

План: N,Б,r

где Т∑r – суммарная наработка на отказ, через которую можно определить статистическую оценку показателей безотказности, например:

План: N,B,r

План: N,Б,T

.

План: N,В,T

.

План: N,Б,(r,T)

Если

то

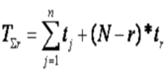
Если

то

План: N,В,(r,T)

Если то

Если то

Алгоритм топологического метода расчета надежности.(Топологический метод расчета надежности)

Метод основан на использовании математического аппарата марковских процессов (вероятность нахождения системы в каком-либо состоянии в будущем не зависит от прошлых состояний системы).

Обозначим Х как множество состояний системы:

,

где xi – i-е состояние, I – множество индексов всех возможных состояний системы, n – количество возможных состояний системы.

Разобьем множество Х на два подмножества:

- подмножество работоспособных состояний системы Х_р;

- подмножество неработоспособных состояний системы .

,

где X_р – подмножество работоспособных состояний системы, I_р – множество индексов работоспособных состояний системы.

,

где – подмножество неработоспособных состояний системы, J – множество индексов неработоспособных состояний системы.

Нахождение системы в том или ином состоянии обусловливает случайный процесс X(t)перехода системы в пространстве ее состояний. X(t) называют также траекторией системы.

Представим X(t) в виде вероятностного графа состояний G(X, W), где Х – множество вершин графа, соответствующих множеству состояний X; W – множество дуг, соединяющих вершины данного графа; P₁(t), ..., P_i(t), ..., P₆(t) – вероятности нахождения системы в i-м состоянии; d(w_ij) – вес дуги w_ij; a_ij – интенсивность перехода из состояния i в состояние j(рис. 2.6).

Если заданы интенсивности a_ij, то, составляя и решая систему уравнений Колмогорова, можно определить вероятности нахождения системы в i-м состоянии P_i(t), а значит и показатели надежности. Однако составление и решение системы уравнений Колмогорова является трудоемкой операцией, поэтому для решения подобных задач применяют топологический метод.

Рис. 2.6. Пример вероятностного графа состояний G(X,W)

Топологический метод использует аппарат теории графов применительно к решению задач надежности. Рассмотрим методику решения задач методом, который позволяет непосредственно по графу состояний G(X, W) без составления и решения уравнений Колмогорова вычислять показатели надежности. Для этого введем некоторые определения.

Прямой путь l^ij из вершины х_i в вершину х_j – цепь последовательно соединенных однонаправленных дуг, где каждая вершина имеет входящую и одну выходящую дуги, за исключением начальной и конечной, имеющих по одной дуге (рис. 2.7).

Рис. 2.7. Определение прямых путей на графе

Вес k-го прямого пути из вершины i в вершину j

,

где - множество дуг, которые составляют k-ый прямой путь.

Замкнутый контурr – прямой путь, на котором начальная и конечная вершины совпадают (рис. 2.8). Вес замкнутого контура r

,

где – множество дуг, входящих в замкнутый контур r.

Рис. 2.8. Примеры замкнутых контуров

Частным случаем замкнутого контура является петля (рис. 2.9), в которой входящая и выходящие дуги сливаются в одну.

Рис. 2.9. Петля

Вес петли при вершине определяется как отрицательная сумма весов дуг, исходящих из этой петли:

где J_n – множество индексов вершин, которые связаны с i-ой вершиной выходящими из нее дугами.

Соединение графа S – это частичный граф, который образуют только замкнутые контуры. Частичный граф представляет собой все вершины, некоторые дуги и петли исходного графа, которые составляют независимые замкнутые контуры (то есть контуры, не имеющие общих вершин). Один граф может располагать несколькими соединениями (рис. 2.10). При образовании соединений следует помнить, что каждая вершина графа G (X, W) имеет петлю.

Рис. 2.10. Пример образования соединения графа

Вес j-го соединения

,

где n – число независимых замкнутых контуров, образующих соединение, R(S_j) – множество независимых замкнутых контуров, образующих соединение.