
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Идея топологического метода расчета надежности систем.
Использ.теория графов и ввод.услов.обознач. Обозначим Х как множество состояний системы:  , где xi – i-е состояние, I – множество индексов всех возможных состояний системы, n – количество возможных состояний системы.
, где xi – i-е состояние, I – множество индексов всех возможных состояний системы, n – количество возможных состояний системы.
Разобьем множество Х на два подмножества: 1) подмножество работоспособных состояний системы Хр;  , где Xр – подмножество работоспособных состояний системы, Iр – множество индексов работоспособных состояний системы. 2) подмножество неработоспособных состояний системы
, где Xр – подмножество работоспособных состояний системы, Iр – множество индексов работоспособных состояний системы. 2) подмножество неработоспособных состояний системы  .
.  . Представим X(t) в виде вероятностного графа состояний G(X, W), где Х – множество вершин графа, соответствующих множеству состояний X; W – множество дуг, соединяющих вершины данного графа; P1(t), ..., Pi(t), ..., P6(t) – вероятности нахождения системы в i-м состоянии; d(wij) – вес дуги wij; aij – интенсивность перехода из состояния i в состояние j. Если заданы интенсивности aij, то, составляя и решая систему уравнений Колмогорова, можно определить вероятности нахождения системы в i-м состоянии Pi(t), а значит и показатели надежности. Однако составление и решение системы уравнений Колмогорова является трудоемкой операцией, поэтому для решения подобных задач применяют топологический метод.
. Представим X(t) в виде вероятностного графа состояний G(X, W), где Х – множество вершин графа, соответствующих множеству состояний X; W – множество дуг, соединяющих вершины данного графа; P1(t), ..., Pi(t), ..., P6(t) – вероятности нахождения системы в i-м состоянии; d(wij) – вес дуги wij; aij – интенсивность перехода из состояния i в состояние j. Если заданы интенсивности aij, то, составляя и решая систему уравнений Колмогорова, можно определить вероятности нахождения системы в i-м состоянии Pi(t), а значит и показатели надежности. Однако составление и решение системы уравнений Колмогорова является трудоемкой операцией, поэтому для решения подобных задач применяют топологический метод. 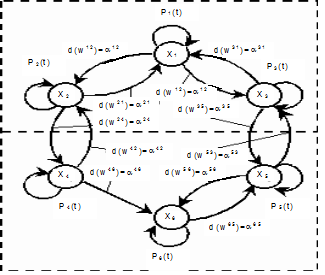
Дата добавления: 2015-01-19; просмотров: 245; Мы поможем в написании вашей работы!; Нарушение авторских прав |