Постановка задачи оптимального резервирования.

Информационные системы состоят из отдельных элементов. Эти элементы с течением времени отказывают и заменяются резервными. Снятые с эксплуатации элементы подвергаются ремонту.

Модель должна определять оптимальный уровень резервных элементов каждого типа. По условию задачи требуется, чтобы система функционировала с максимальной надежностью. Если какой-нибудь элемент отказывает, то его заменяют запасным из числа резервных. Отказавший элемент сразу начинают ремонтировать. В системе непрерывно должно функционировать ZK элементов K-го типа, причем в запасе должно иметься XK элементов того же K-го типа

.

Сущность задачи заключается в оптимальном распределении стоимостных или каких-либо других ресурсов , выделенных на приобретение резервных единиц.

Рассматриваемая система считается отказавшей, если в момент отказа работающего элемента K-го типа все XK запасных элементов того же типа находятся в ремонте. Таким образом, надо найти количество резервных элементов

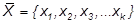
так, чтобы вероятность нехватки резервных элементов была минимальной.

Введем обозначения:

- показатель надежности всей системы (вероятность безотказной работы системы);

- вероятность безотказной работы K-го элемента.

Так как модель соединений элементов с точки зрения надежности представляется как последовательное соединение элементов, то справедлива формула

Можно сформулировать задачу на минимум: необходимо найти минимум риска нехватки элементов

На все элементы есть ограничения (вес, цена, объем и т.д.). Но мы будем пользоваться только стоимостным ограничением, как, пожалуй, наиболее часто встречающимся, хотя задача решается и для нескольких ограничений.

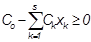
где

- стоимость одного элемента k-го типа.