Многочлен Лагранжа.

Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n+1 пар чисел (x₀, y₀), (x₁, y₁),…, (x_n, y_n), где все x_j различны, существует единственный многочлен L(x) степени не более n, для которого L(x_j) = y_j.

В простейшем случае (n=1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

Лагранж предложил способ вычисления таких многочленов:

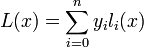
где базисные полиномы определяются по формуле:

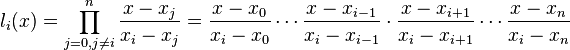
l_i(x) обладают следующими свойствами:

• являются многочленами степени n
• l_i(x_i) = 1
• l_i(x_j) = 0 при j ≠ i

Отсюда следует, что L(x), как линейная комбинация l_i(x), может иметь степень не больше n, и L(x_i) = y_i.

Используя полином Лагранжа можно показать, что

если 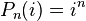, то первые два по старшинству коэффициента многочлена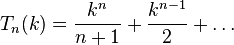

Указанная выше сумма задаёт биективное отображение между 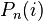и

Полиномы Лагранжа используются для интерполяции, а также для численного интегрирования.

Пусть для функции f(x) известны значения y_i=f(x_i) в некоторых точках. Тогда мы можем интерполировать эту функцию как

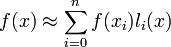
В частности,

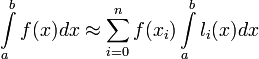
Значения интегралов от l_i не зависят от f(x), и их можно вычислить заранее, зная последовательность x_j.