Описание алгоритма. Задача заключается в нахождении корней нелинейного уравнения

Задача заключается в нахождении корней нелинейного уравнения

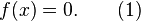
Для начала итераций необходимо знать отрезок значений , на концах которого функция принимает значения противоположных знаков.

Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:

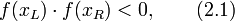
в действительных вычислениях такой способ проверки противоположности знаков при крутых функциях приводит к преждевременному переполнению.

Для устранения переполнения и уменьшения затрат времени, то есть для увеличения быстродействия, на некоторых программно-компьютерных комплексах противоположность знаков значений функции на концах отрезка нужно определять по формуле:

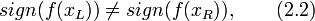
так как одна операция сравнения двух знаков двух чисел требует меньшего времени, чем две операции: умножение двух чисел (особенно с плавающей запятой и двойной длины) и сравнение результата с нулём. При данном сравнении, значения функции в точках 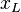и можно не вычислять, достаточно вычислить только знаки функции в этих точках, что требует меньшего машинного времени.

Из непрерывности функции и условия (2.2) следует, что на отрезке существует хотя бы один корень уравнения (в случае не монотонной функции функция имеет несколько корней и метод приводит к нахождению одного из них).

Найдём значение в середине отрезка:

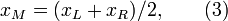
в действительных вычислениях, для уменьшения числа операций, в начале, вне цикла, вычисляют длину отрезка по формуле:

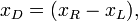
а в цикле вычисляют длину очередных новых отрезков по формуле: и новую середину по формуле:

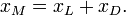
Вычислим значение функции в середине отрезка :

• Если или, в действительных вычислениях, 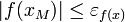, где — заданная точность по оси , то корень найден.
• Иначе или, в действительных вычислениях, , то разобьём отрезок на два равных отрезка: и .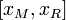

Теперь найдём новый отрезок, на котором функция меняет знак:

• Если значения функции на концах отрезка имеют противоположные знаки на левом отрезке, или , то, соответственно, корень находится внутри левого отрезка . Тогда возьмём левый отрезок присвоением , и повторим описанную процедуру до достижения требуемой точности по оси .
• Иначе значения функции на концах отрезка имеют противоположные знаки на правом отрезке, или , то, соответственно, корень находится внутри правого отрезка 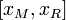. Тогда возьмём правый отрезок присвоением , и повторим описанную процедуру до достижения требуемой точности по оси .

За количество итераций деление пополам осуществляется раз, поэтому длина конечного отрезка в раз меньше длины исходного отрезка.

Существует похожий метод, но с критерием останова вычислений 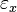по оси ^[1], в этом методе вычисления продолжаются до тех пор, пока, после очередного деления пополам, новый отрезок больше заданной точности по оси : . В этом методе отрезок на оси может достичь заданной величины 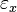, а значения функций (особенно крутых) на оси могут очень далеко отстоять от нуля, при пологих же функциях этот метод приводит к большому числу лишних вычислений.

В дискретных функциях и — это номера элементов массива, которые не могут быть дробными, и, в случае второго критерия останова вычислений, разность не может быть меньше .