Геометрическая интерпретация

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Пусть — определённая на отрезке и дифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:

где 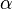— угол наклона касательной в точке .

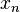Следовательно искомое выражение для 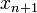имеет вид:

Итерационный процесс начинается с некоего начального приближения (чем ближе к корню, тем лучше, но если предположения о его нахождении отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).