Обоснование. Чтобы численно решить уравнение методом простой итерации, его необходимо привести к следующей форме:

Чтобы численно решить уравнение 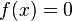методом простой итерации, его необходимо привести к следующей форм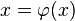е: , где — сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения 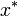должно выполняться условие 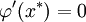. Решение данного уравнения ищут в виде , тогда:

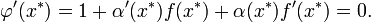
В предположении, что точка приближения «достаточно близка» к корню 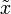, и что заданная функция непрерывна , окончательная формула для 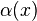такова:

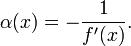
С учётом этого функция 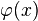определяется:

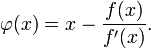
При некоторых условиях эта функция в окрестности корня осуществляет сжимающее отображение^[1], и алгоритм нахождения численного решения уравнения 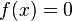сводится к итерационной процедуре вычисления:

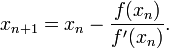
По теореме Банаха последовательность приближений стремится к корню уравнения .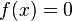

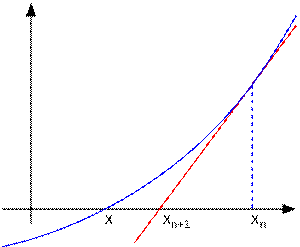
Иллюстрация метода Ньютона (синим изображена функция 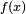, нуль которой необходимо найти, красным — касательная в точке очередного приближения ). Здесь мы можем увидеть, что последующее приближение 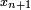лучше предыдущего .