Линейная алгебра и аналитическая геометрия

1. Определение матрицы размера m×n.

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.

2. Определения квадратной, треугольной, диагональной и единичной матриц.

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпдают:m=n. Число m=n называется порядком квадратной матрицы.

Квадратная матрица А порядка n×n называется верхней треугольной матрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т.е. a_ij=0, при всех i>j.

Квадратная матрица А порядка n×n называетсянижней треугольнойматрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i<j.

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю.

Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей и обозначается через E или E ⁿ, где n - порядок матрицы.

3. Определение равенства матриц.

Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a_ij = b_ij. Так если и , то A=B, если a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁ и a₂₂ = b₂₂.

4. Операции сложения матриц и умножения матрицы на число.

Сложение: Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,

или

Умножение матрицы на число: Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .

Для любых чисел a и b и матриц A и B выполняются равенства:

1.

2.

3. .

5. Операция умножения матриц.

Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:

.

Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c₁₃, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.

В общем случае, если мы умножаем матрицу A = (a_ij) размера m×n на матрицу B = (b_ij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент c_ij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.

Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.

Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,

.

6. Операция транспонирования матрицы.

Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если 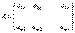, то .

Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.

Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают A^T.

Связь между матрицей A и её транспонированной можно записать в виде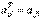

7. Определение перестановки и инверсии в ней.

Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3, . . . , n в строчку одно за другим. Говорят, что в данной перестановке два числа образуют инверсию (беспорядок), если большее из чисел в данной перестановке стоит левее меньшего. В противном случае эти два числа образуют порядок.

8. Теорема о числе перестановок.

Теорема 7.2 (о числе перестановок). Число всех перестановок множества из n элементов определяется формулой 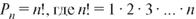(считаем, что по определению

Пример 3. Цифры 0, 1, 2, 3 записаны на 4-х карточках. Сколько различных 4-значных цифр можно составить из этих карточек?

Решение. Число различных комбинаций из 4-х цифр равно 4!; 3! комбинаций, начинающихся с 0, следует исключить. В результате количество различных 4-значных чисел равно 4! - 3! = 18.

Определение. Упорядоченные наборы, состоящие из k элементов, взятых из данных n элементов, называются размещениями из n элементов по k.