Из определения следует, что обратная матрица B будет квадратной матрицей того же порядка, что и матрица A(иначе одно из произведений AB или BA было бы не определено).

Обратная матрица для матрицы A обозначается . Таким образом, если существует, то .

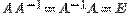Из определения обратной матрицы следует, что матрица A является обратной для матрицы , то есть . Про матрицы A и можно говорить, что они обратны друг другу или взаимно обратны.

30. Условие существования обратной матрицы.

Если определитель матрицы равен нулю, то обратная к ней не существует. Квадратную матрицу A назовем вырожденной или особенной матрицей, если , и невырожденной или неособенной матрицей, если .

Если квадратная матрица A является невырожденной, то обратная для нее существует и (1) где 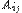- алгебраические дополнения к элементам .

Обратная матрица для квадратной матрицы A существует тогда и только тогда, когда матрица A - невырожденная, обратная матрица единственна, и справедлива формула (1).

31. Правило вычисления обратной матрицы.

Найти обратную матрицу для матрицы

Алгоритм точно такой же, как и для случая «два на два».

Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .