Отсюда следует, что система векторов ЛЗ.

42. Определение линейного пространства.

Непустое множество Е элементов любой природы Е = { x, y, z, t, … } называется линейным или векторным пространством над полем действительных чисел R , если выполняются следующие условия:

а) имеется правило, посредством которого любым двум элементам х, у множества Е ставится в соответствие элемент z этого же множества Е, называемый суммой этих элементов : z = x + y;

b) имеется правило, посредством которого каждому элементу х множества Е и любому действительному числу λ ставится в соответствие элемент u = λ x , называемый произведением х на λ .

При этом указанные правила ( операции ) удовлетворяют восьми аксиомам:

1) x + y = y + x - коммутативное ( переместительное ) свойство суммы ;

2) ( x + y ) + z = x + (y + z ) - ассоциативное ( сочетательное ) свойство суммы;

3) Существует нулевой элемент 0 Є Е такой, что х + 0 = х для любого элемента х Є Е ;

4) Для любого элемента х Є Е существует противоположный элемент (- х ) Є Е такой, что х + ( - х ) = 0 ;

5) Для любых действительных чисел α и β верно равенство α(βх) = (αβ)х - ассоциативное относительно числового множителя свойство ;

6) 1∙х = х для любого элемента х Є Е ( особая роль числового множителя 1 );

7) Для любого действительного λ и произвольных элементов х, у Є Е выполняется равенство λ ( х + у ) = λ х +λ у - дистрибутивное (распределительное) относительно суммы элементов свойство;

8) Для любых действительных чисел α и β и произвольного элемента хЄ Е верно равенство (α + β ) х = α х + β х - дистрибутивное (распределительное) относительно суммы числовых множителей свойство.

43. Примеры линейных пространств.

Примеры линейных пространств

1. Множество всех алгебраических многочленов степени, не превышающей натурально го числа n. Легко убедиться, что если х и у - многочлены степени не выше n,то они будут обладать свойствами 1 – 8 ;

2.Множество геометрических векторов пространства R², исходящих из начала координат;

3. Множество всех матриц одного и того же размера m×n с введенными в нем операциями сложения матриц и умножения матрицы на число . В этом множестве нулевая матрица будет нулевым элементом. Матрица, полученная из матрицы А умножением всех ее элементов на число ( - 1), будет являться для матрицы А противоположным элементом ;

4. Множество всех функций, непрерывных на отрезке [ a , b ], с поточечными для функций операциями сложения и умножения на число.

5. Множество всех функций вида αе^t+be^-t, где α и b – произвольные вещественные числа.

44. Определение базиса линейного пространства.

Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.

45. (*)Канонический базис n-мерного линейного пространства.

Вещественное линейное пространство L называется евклидовым, если в нём задана положительно определённая квадратичная форма. Это означает, что одна из квадратичных форм выделена и играет особую роль (играет роль выбора масштаба измерения) . Будем называть эту выделенную положительно определенную квадратичную форму основной квадратичной формой. Иначе можно сказать, что если в качестве основной квадратичной формы выбрана та, которая в стандартном базисе арифметического пространства (состоящем из столбцов единичной матрицы порядка n ) то базис имеет канонический вид.

46. Определение подпространства.

Линейное подпространство или векторное подпространство ― непустое подмножество K линейного пространства V такое, что K само является линейным пространством по отношению к определенным в Vдействиям сложения и умножения на скаляр. Множество всех подпространств обычно обозначают как Lat(V). Чтобы подмножество было подпространством, необходимо и достаточно, чтобы

1. для всякого вектора , вектор также принадлежал K, при любом ;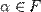

2. для всяких векторов 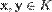, вектор 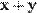также принадлежал K.

Последние два утверждения эквивалентны следующему: для всяких векторов , вектор также принадлежал K для любых .

47. Теорема о разложении вектора по базису в линейном пространстве.