
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определитель произведения двух квадратных матриц равен произведению определителей сомножителей.
24. Определение минора порядка k.
Ранг матрицы— Рангом системы строк (столбцов) матрицы строк и столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие
25. Определение минора  элемента
элемента  .
.
Минором элемента определителя называется определитель, полученный из исходного определителя вычеркиванием той строки и того столбца, которым принадлежит данный элемент. Обозначают минор элемента  через
через  .
.
26. Определение алгебраического дополнения  элемента
элемента  .
.
Алгебраическим дополнением к элементу  матрицы
матрицы  называется число, равное
называется число, равное  , где
, где  - определитель матрицы, полученной из матрицы вычеркиванием i-ой строки и j-ого столбца. Алгебраическое дополнение к элементу
- определитель матрицы, полученной из матрицы вычеркиванием i-ой строки и j-ого столбца. Алгебраическое дополнение к элементу  матрицы
матрицы  обозначается
обозначается 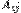 .
.
27. Теорема Лапласа о вычислении определителя порядка n.
Пусть выбраны любые n строк матрицы A. Тогда определитель матрицы A равен сумме всевозможных произведений миноров n-го порядка, расположенных в этих строках, на их алгебраические дополнения.

где суммирование ведётся по всевозможным номерам столбцов 
28. Теорема о сумме произведений элементов одной строки на алгебраические дополнения элементов другой строки.
Определитель матрицы равен сумме произведений элементов некоторого ряда (строки или столбца) определителя на их алгебраические дополнения. Иначе говоря, справедливы следующиеформулы разложения определителя поj-й строке(илипо элементамj-й строки): 
иразложения определителя поk-му столбцу: 
для любых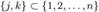 .
.
29. Определение обратной матрицы.
Матрица B называется обратной матрицей для квадратной матрицы A, если AB=BA=E.
Дата добавления: 2015-01-19; просмотров: 272; Мы поможем в написании вашей работы!; Нарушение авторских прав |