Методика расчета конструкций по предельным состояниям

Расчетные формулы для подбора сечений и проверки несущей способности конструкций по первому предельному состоянию получаются из основного неравенства

N £ S, (3.1)

где: N - усилие, действующее в рассчитываемом элементе конструкции (функция нагрузок и других воздействий);

S - предельное усилие, которое может воспринять рассчитываемый элемент (функция физико-механических свойств материала, условий работы и размеров элемента).

Так как внешние воздействия (нагрузки F) могут изменяться в широких пределах, то в СНиПах различают расчетные (наибольшие) величины «F» и нормативные «F_n» (нормального режима эксплуатации)

F = F_n· g_f . (3.2)

F_n принимаются по СНиП 2.01.07-85 "Нагрузки и воздействия", а коэффициент надежности по нагрузке (g_f) определяется уровнем обеспеченности w(F₀) = 0.999, т.е. допускается всего 0.1% случаев превышения рассматриваемой нагрузки за весь период эксплуатации сооружения. Таким образом, по СНиП, g_f колеблется от 1.05 - для массы металлических конструкций, до 1.6 - для снега.

Обычно, на конструкции действуют одновременно несколько видов нагрузок. Поэтому, в методике предельных состояний, это учитывается коэффициентом сочетаний y £ 1, на который следует умножать каждую из суммируемых нагрузок. Согласно СНиП y колеблется от 1 до 0.6 и менее - для особых случаев.

Кроме того, надежность сооружения должна соответствовать его назначению и степени ответственности. По этим характеристикам сооружения разделены на 3 класса. С этой целью введен коэффициент надежности по ответственности: для первого класса g_n = 0.95¸1.2, для второго – g_n = 0.95, для третьего – g_n = 0.8¸0.95.

Таким образом, левую часть неравенства (3.1) можно записать

N = g_n· 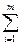F_ni·g_fi·y_i· (3.3)

где – усилие в элементе от единичной нагрузки;

m – число одновременно учитываемых нагрузок.

В правой части неравенства (3.1) S зависит, в первую очередь от нормативного (R_n) и расчетного (R_у) сопротивлений материала, которые связаны между собой с помощью коэффициента надежности по материалу g_m соотношением

R_у = R_n /g_m. (3.4)

В качестве R_n принимается минимальные s_т или s_u, с обеспеченностью 0.95 (95%). При нормальном законе распределения это достигается уменьшением среднего значения сопротивления на 1.64 стандарта, т.е.

R_u = R_u – 1.64·s. (3.5)

Значения g_m по СНиП находятся в пределах 1.025 до 1.100.

Рассмотренные коэффициенты g_f, g_n, y и g_m не исчерпывают весь комплекс факторов, определяющих напряженное состояние конструкций. Так, не учитывают переменность во времени, нагрузки, внезапный и ударный характер ее воздействия, концентрации напряжений, случайные эксцентриситеты нагрузок, влияние низких и высоких температур, условность расчетной схемы и множество других факторов.

Для их учета вводится коэффициент условий работы g_с = 0.7¸1.2, на который умножается R_y и дифференцирован по видам элементов и характеру воздействий.

Таким образом, окончательно неравенство (3.1) первого предельного состояния может быть записано

N = g_n· 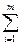F_ni·g_fi·y_i· £ А·R_u·g_с/g_m = S, (3.6)

где А - геометрическая характеристика поперечного сечения элемента (площадь, момент сопротивления и т.п.).

Предельные состояния первой группы проверяются расчетом на максимальные расчетные нагрузки.

Вторая группа предельных состояний проверяется по нормативным (эксплуатационным нагрузкам). Неравенство предельного состояния имеет вид:

g_n· 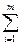F_ni·y_i·d_i £ D, (3.7)

где d_i - перемещение конструкции от единичного воздействия;

D - предельная величина перемещения, устанавливаемая нормами, либо проектным заданием.