В) Основы работы и расчета на устойчивость центрально сжатых стержней

Длинные гибкие стержни исчерпывают несущую способность от потери устойчивости и характеризуются приведенным графиком (рисунок 3.5 б).

При этом, с ростом нагрузки, стержень находится в устойчивом состоянии при N < N_сr, при N = N_сr - стержень начинает резко выпучиваться и в неустойчивом при N > N_сr - теряет несущую способность.

а – расчетная схема; б – зависимость между нагрузкой и прогибом стержня   Рисунок 3.5 Работа центрально-сжатого стержня

Строгое определение этих состояний даются на основе энергетических принципов.

При фиксированном N = const, давая стержню возможное перемещение, подсчитываются приращения внешних сил d·N_e и внутренних d·N_i сил.

Если, d·N_i > d·N_e - устойчивое состояние, при d·N_i < d·N_e неустойчивое, при

d·N_i = d·N_e - критическое.

Сила N = N_сr", при которой стержень теряет несущую способность (устойчивость) называется критической.

При описании устойчивости стержней, приращения работ на возможных перемещениях можно заменить приращениями соответствующих моментов d×M_e и d×M_i.

Рассмотрим два случая:

I. Для идеально упругого и прямолинейного стержня при N=const dM_e=N×V (V - амплитута прогиба), а dM_i =r·EJ, (r=-у") - кривизна. Задавая форму возможного перемещения стержня по синусоиде у = -V·sin px/l_o, получаем r=-у" (x=l_o/2= p²·V/l_o²). Подставляя это значение в dM_i иdM_e и приравнивая dM_i=dM_e получим значение первой критической силы (формула Эйлера 1744г.)

N'_cr=p²·EJ/l_o², (3.22)

тогда, критическое напряжение будет равно

s_cr= , (3.23)

где ; l=l_o/i; l_o= m·l - расчетная длина стержня;

m - коэффициент приведения, зависящий от способа закрепления концов стержня.

Эта формула справедлива при Е = const, т.е. s_cr£s_пц т.к. l³p 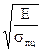и s_пц=20 кН/см², то l ³ 100. Для сталей повышенной прочности применимость (3.23) ограничена l ³ 85.

II. При l меньше предельных, стержни теряют устойчивость в упруго-пластической стадии с касательным модулем упругости Е_t = ds/dε <E. Для этого случая проф. Ясинский Ф.С. предложил следующую схему работы стержня при потере устойчивости: N = const, равномерное распределение s по сечению s_o = N/A > s_пц (рисунок 3.6).

При прогибе стержня с амплитудой "V", на сжатой стороне "s" будут увеличиваться в соответствии с Е_t, а на противоположной стороне на сжатие от N накладывается растяжение от изгиба, т.е. произойдет разгрузка, которая следует упругому закону s = ε·Е. Поэтому, эпюра s будет ассиметричной, нейтральная ось переместится и появится дополнительный эксцентриситет "а" силы N.

Тогда, приращение момента внешней силы будет

δМ_е = N·(V + a), (3.23)

а для внутренних сил приращение определится суммой интегралов по площадям А₁ и А₂:

δМ_i = s₁·y·dA + s₂·y·dA = ρ·(E·J₁ + E·J₂) = ρ·T·J, (3.24)

где Т = (EJ₁ + EJ₂) / J - приведенный модуль деформации.

Тогда, из равенства δМ_е = δМ_i получим формулу для s_cr

s_cr = (3.25)

или s_cr = ; (3.26)

где: λ_ef = ; i_ef = .

Если, деформация сжатия в процессе продольного изгиба растет или остается постоянной, т.е. разгрузка не происходит, то всё сечение находится в пластическом состоянии, характеризуемом касательным модулем деформации Е_t, тогда

s_cr = 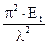. (3.27)

а – эпюра напряжений; б – поперечное сечение стержня   Рисунок 3.6 - Напряженно-деформированное состояние центрально сжатого стержня в момент потери устойчивости

Так как, на практике не существует идеально прямых стержней и идеальных условий центрального приложения силы N, то в практических расчетах вводится некоторый эквивалентный эксцентриситет сжимающей силы е_ef, который зависит от технологии изготовления, транспортировки, монтажа, решения узлов и т.д.

Поэтому, по I-му предельному состоянию устойчивость сжатого стержня будет обеспечена, если s = £ s_cr·γ_c. Умножив и поделив правую часть на R_y и введя обозначение

= φ, (3.28)

называемое коэффициентом устойчивости (продольного изгиба) получим

s = < φ·R_y·γ_c или 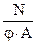< R_y·γ_c. (3.29)

Коэффициент φ имеет двойственную природу:

φ = = · = φ₁·φ₂, (3.30)

φ₁ зависит от гибкости и марки стали

φ₁ = , (3.31)

где - условная гибкость.

В упругой стадии Т = Е, значит φ₁ = .

Коэффициент φ₂ зависит от λ, а наименьшее его значение соответствует средней λ =100.

Коэффициент φ принимается по таблице 72 СНиП или подсчитывается по формулам 8, 9 или 10 СНиП

при 0 < £ 2.5 – φ = 1 – 0.066· · ; при 2.5 < £ 4.5 – φ = 1.46 – 0.34· + 0.021· 2; при > 4.5 – φ = .

(3.32)

При этом, для учета формы сечения, все стержни разделены на 3 группы: