Критическую силу можно определить используя известные выражения

d·N₁ = d·N₂, либо δМ_i = δM_e. Условие критического состояния можно видеть из диаграмм М_i = и M_e = N·(e + f) и соответствует точке касания "m", где

s_u = ρ·y·E_S, ρ = – кривизна, E_S = s/ε – секущий модуль деформаций.

а – расчетная схема; б – зависимость между нагрузкой и прогибом стержня Рисунок 3.8 - Работа внецентренно сжатого стержня

Прогиб определяется из условия равновесия M_e = М_i

M_e = N·(e + f) и M_i = ρ·E·J_S

f = , (3.34)

Задавая y = -f·sin(π·x/l), - форма изогнутой оси стержня, получаем значение кривизны ρ.

В результате подстановок получим искомое соотношение

ε = ε_o + . (3.35)

Решая систему полученных уравнений, можно получить значение длины стержня "l", при которой заданная нагрузка N будет критической, уменьшающаяся с увеличением "е". Критическая сила зависит также от формы сечения стержня, учитываемая коэффициентом влияния формы сечения η, который в свою очередь зависит от относительного эксцентриситета m = e/ρ (где ρ = W/A - ядровое расстояние) и условной гибкости .

Для практических расчетов вводится понятие приведенный эксцентриситет

m_ef = m·η. (3.36)

а – эпюры напряжений; б – поперечное сечение стержня Рисунок 3.9 - Напряженно-деформированное состояние внецентренно сжатого стержня в момент потери устойчивости		Рисунок 3.10 - Условие критического состояния внецентренно сжатого стержня

Таким образом, формула проверки устойчивости внецентренно сжатых стержней записывается

£ R_y·γ_c, (3.37)

где φ_e = s_cr.e/R_y – коэффициент устойчивости, зависящий от m_ef и (по таблицам и графикам СниПа).

С точки зрения экономии металла, в рассматриваемых стержнях, целесообразно развивать сечение в направлении эксцентриситета, но при этом, возрастает опасность потери устойчивости стержня в перпендикулярном направлении - относительно оси "у".

В связи с этим, в формулу проверки устойчивости вводится понижающий коэффициент "с"

£ R_y·γ_c, (3.38)

где с = N_cr·M/N_cr = φ_у·M/φ_у; с= f (m_x=e/ρ_x, формы сечения, λ_у);

φ_у и N_cr – коэффициент устойчивости и критическая сила для центрально сжатого стержня.

е) Проверка на усталостностьпроизводится по формуле

s_max £ α·R_v·γ_v, (3.39)

при ограничении

α·R_v·γ_v £ R_u/γ_u; γ_u = 1.3, (3.40)

где R_v – условное расчетное сопротивление усталости.

Для 1-й и 2-й групп элементов (номер группы определяется по концентрации напряжений)

α = 0.064·(n/10⁶)² – 0.5·(n/10⁶) + 1.75; (3.41)

для 3-й - 8-й групп элементов

α = 0.07·(n/10⁶)² – 0.64·(n/10⁶) + 2.2; (3.41)

при n > 3.9·10⁶ циклов α = 0.77,

γ_v = 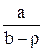- коэффициент влияния ассиметрии цикла;

где а и b = f(ρ и знака усилия);

ρ = s_min/s_max = -1 при n = 2·10⁶.

Таким образом α, меняется от 0.77 до 2.14; 1 £ γ_v < ¥; и R_v – от 2.7 до 14.5 кН/см² в зависимости от группы элемента и типа стали.

Проведенные подсчеты показывают, что вибрационная прочность может уменьшаться в 13.5 - 23 раза в зависимости от режима нагружения, типа стали и концентрации напряжений.

Так, для примера, подкрановая ферма с нижним поясом из L100х10 (8-я группа элементов) имеет вибрационную прочность α·R_v·γ_v = 5.4 кН/см².

(R_v = 2.7 кН/см²; α = 3.31 и γ_v =1.67) и подкрановая балка из сварного двутавра - α·R_v·γ_v = 66.3 кН/см². (R_v = 10 кН/см²; α = 3.31 и γ_v =1.67), т.е. в 8.7 раза выше вибрационной прочности подкрановой фермы.

ж) Проверка хладостойкостипроизводится по формуле

s_max £ β ·γ_с·R_u/γ_u, (3.42)

где b - коэффициент понижения R.

При эксплуатационной t^о ³ t₁, обеспечивается вязкое разрушение стали, тогда β = 1. При t < t₂ сталь разрушается хрупко, эксплуатация конструкции недопустима. При t = t₂ расчетное сопротивление снижается на 20-30% в зависимости от типа стали и толщины проката.

Экспериментально установлено при t = t₂ – β = 0.7÷0.8,

при t₂ < t < t₁ - β = 1÷(0.7÷0.8),

β = 1 – α · ; (3.43)

t₁ и t₂ - критические температуры.

Рассмотрим расчетное сопротивление хладостойкости для элементов фермы прикрепленных в узлах к фасонке 10 мм для районов Москвы и Новосибирска с расчетными t = -26^oС и t = -39^oС, сталь С245 (ВСт3пс6).

При t < 20 мм имеем α = 0.25. Критические t₁ = -12.5^оС, t₂ = -32.5^оС, γ_с = 1, γ_n = 1.3. Тогда для Москвы β = 0.86, для Новосибирска β = 0.67.

Таким образом, хладостойкость для Москвы –23.8 кН/см² - совпадает с R_y = 24 кН/см², для Новосибирска – 18.6 кН/см² - снижена на 30%.