Б) Основа работы и расчета изгибаемых элементов

В соответствии с гипотезой плоских сечений Бернулли, изменение деформаций по высоте сечения балок происходит по линейному закону, напряжения распределяются аналогично только до s_т (рисунок 3.1).

Напряжения в точках, находящихся на расстоянии "у" от нейтральной оси, определяются по формуле

s = 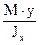. (3.11)

Рисунок 3.2 – Изменение эпюры напряжений в изгибаемом элементе при

развитии пластических деформаций в материале

Максимальное s возникает в крайней фибре сечения, при у = h/2

s_max = , (3.12)

где W_x = J_х·2/h - момент сопротивления,

т.е. s_max = . (3.13)

Таким образом, проверка прочности изгибаемых элементов, работающих в пределах упругих деформаций по первому предельному состоянию, производится по следующим формулам

s_max = £ R_y·g_c и t_max = 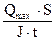£ R_s·g_c. (3.14)

По второму предельному состоянию наибольший прогиб балки от нормативной равномерно распределенной нагрузки сравнивается с предельной величиной прогиба по СНиП 2.01.07-85 "Нагрузки и воздействия".

f_max = £ f_u. (3.15)

Для балок, загруженных сосредоточенной силой Р_n в середине пролета, проверка осуществляется по формуле

f_max = 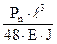£ f_u. (3.16)

Появление фибровой текучести не исчерпывает несущую способность элемента, т.к. в глубине сечения s < s_т и стержень будет оказывать сопротивление при росте нагрузки.

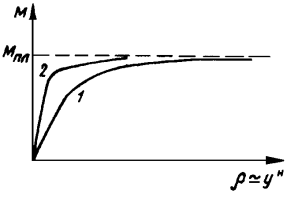
Это приведет к росту деформаций, а рост s будет ограничен s_т и упругое ядро будет уменьшаться. Кривизна "r" » "у", а значит прогиб балки "у" будет резко нелинейно возрастать (рисунок 3.3), а несущая способность асимптотически приближаться к предельной М_пл. Эта стадия называется упругопластической, график деформаций вырождается в горизонтальную линию (e®±¥), но практически это невозможно, т.к. материал обладает ограниченной деформативностью e_lim, после которой происходит разрушение при a_min > 0. Поэтому, с небольшой погрешностью (для упрощения), можно использовать предельную эпюру (рисунок 3.2. в).

Кинематически эта стадия соответствует шарнирному механизму, т.е. возможен взаимный поворот частей балок, разделенных рассматриваемым сечением.

Рисунок 3.3 - Рост кривизны балки прямоугольного сечения (1) и двутавровой балки (2) при развитии в материале пластических деформаций

Поэтому, условный шарнир, получил название пластический шарнир, определяющий предельную несущую способность изгибаемого элемента. В отличие от механического, пластический шарнир исчезает, как только «М» меняет направление, т.к. материал при этом восстанавливает упругие свойства.

Предельный момент в шарнире пластичности определяется

М_пл = s_т· 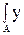·dA = s_т·( + ) = s_т·W_пл, (3.17)

где W_пл = 2·S - пластический момент сопротивления.

Введем коэффициент:

с = W_пл/W = М_пл/M, (3.18)

характеризующий резерв несущей способности балки, или иногда, называют коэффициентом, учитывающий степень развития пластических деформаций и зависящий от формы сечения.

Значения коэффициента "с": для прямоугольного - с = 1.5; прокатного двутавра - с = 1.1 и составного двутавра - с = 1.2 – 1.04.

Распределение пластических деформаций по длине балки зависит от типа опор и характера распределения нагрузки по ее длине (рисунок 3.4).

Таким образом, проверка прочности изгибаемых элементов при наличии пластических деформаций (для сталей R_y < 530 мПа) производится по формулам

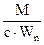£ R_y·g_c или £ R_y·g_c×с. (3.19)

При многокомпонентном напряженном состоянии проверку прочности балки выполняют по формуле

s_пр = £ 1.15 ·R_у·g_с, (3.20)

где 1.15 – коэффициент, учитывающий развитие пластических деформаций.

Формулы (3.19) СНиП допускают использовать при наличии двух компонент s_х и t_ху, когда t_ху < 0.5·R_S, а при большем значении t_ху знаменатель умножается на коэффициент b < 1, зависящий от t.

а – расчетная схема балки: б – эпюры напряжений в различных сечениях балки: в – эпюры изгибающих моментов; 1 – зона пластических деформаций; МI – предельная эпюра при упругой работе материала; МII – то же, при появлении пластического шарнира

Рисунок 3.4 - Распределение пластических деформаций в балке

При изгибе относительно двух главных осей (косой изгиб) проверку прочности с учетом пластических деформаций осуществляют по формуле

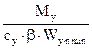+ £ R_y·g_c при t £ 0.5·R_S. (3.21)