Методы определения порядка реакции и константы скорости.

Определение порядка реакции открывает возможности выяснения вероятного механизма химического процесса. Для определения порядка реакций применяются различные методы:
1. Метод подстановки (аналитический метод). Экспериментально находят концентрации одного из веществ с через разные промежутки времени от начала реакции. Значения с, и начальной концентрации с0 подставляют в уравнение (2.4.) и рассчитывают константу скорости. Если величина k, вычисленная для разных моментов времени, остается практически постоянной, это говорит о том, что реакция первого порядка. Если значения k не сохраняют постоянного значения, величины с и с0 подставляют в уравнение (2.5.). Постоянство значений k свидетельствует о втором порядке реакции.
2. Графический метод. Из уравнения (2.4.) следует, что график зависимости lnс от времени должен иметь вид прямой линии (рис.2.1 а.). Тангенс угла наклона прямой по отношению к оси абцисс равен – k, а отрезок, отсекаемый прямой на оси ординат равен lnс0. Из уравнения (2.5.) следует, что зависимость 1/с от времени выражается прямой линией с тангенсом угла наклона, равным k (рис.2.1 б.). Отрезок, отсекаемый прямой на оси ординат равен 1/с0. Для определения порядка реакции графическим методом, полученные экспериментально значения с, наносят на график в координатах "lnс-t ". Если получается прямая линия – это означает, что реакция имеет первый порядок. Если в этих координатах прямая линия не получается, строят график 1/с =f(t).График,подобный представленному на рис.2.1 б,. говорит о том, что реакция второго порядка.

Константа скорости реакции зависит от природы реагирующих веществ, температуры, присутствия и концентрации катализаторов и – в растворах– от природы растворителя. Все это делает константу скорости химической реакции важнейшей характеристикой процесса, которая весьма точно описывает его свойства и позволяет осуществлять классификацию различных процессов по характерным для них константам скоростей реакций. Константы скорости реакций вычисляют из опытных данных с помощью
кинетических уравнений. Важным видом представления экспериментальных данных являются кинетические кривые. Эти кривые изображают экспериментальные
зависимости концентрации выбранного реагента от времени. Вид этих кривых может быть весьма разнообразным. Касательные к этим кривым позволяют определить скорость химической реакции в данный момент времени. Понятно, что скорость химической реакции постоянно меняется, так как меняется концентрация реагентов. Сложные реакции подразделяют на одновременные или
параллельные, последовательные и сопряженные (каталитические). Каталитические реакции, как и цепные, можно рассматривать, как последовательные с периодом индукции (ожидания) и с чередованием активных частиц.

43 (6) Зависимость скорости реакции от температуры . Физическую сущность k раскрывает зависимость, установленная в 1884 г. Я. Вант-Гоффом из молекулярно-кинетических представлений для элементарных химических реакций, известная как уравнение Аррениуса: 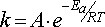где предэкспоненциальный множитель А – постоянная Аррениуса (частотный фактор), связанная с частотой столкновения молекул, участвующих в реакции и их ориентацией в пространстве, может быть вычислена теоретически из молекулярно-кинетической теории или статистической термодинамики; Еа – по С. Аррениусу (1889 г.) энергия активации, ранее рассматривалась в химической кинетике как эмпирическая постоянная, не зависящая от температуры. В настоящее время появилась возможность ее приближенной оценки с помощью методов квантовой химии; R – универсальная газовая постоянная, равная 8,313 Дж/(моль×К); Т–термодинамическая температура, К.
Влияние на скорость реакции температуры С.Аррениус трактовал как сдвиг равновесия между неактивными и активными молекулами. (Основной вклад С.Аррениуса в развитие химической кинетики состоит во введении представлений об энергии активации как потенциальном барьере, который должны преодолеть реагирующие молекулы прежде, чем стать продуктами реакции).
Как видно из уравнения Аррениуса, зависимость скорости химической реакции (u @ k) от температуры имеет экспоненциальный характер, что согласуется с концепцией «активных частиц» и теорией «активных столкновений» в химической кинетике. Энергию активации в простейшем варианте можно определить по константам скорости при двух разных температурах: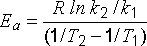

Зависимость скорости химической реакции от температуры в небольшом интервале температур описывает эмпирическое правило Вант-Гоффа: при изменении температуры на каждые 10 градусов скорость большинства химических реакций изменяется в 2–4 раза.Математическое выражение правила Вант-Гоффа: 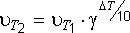где и – скорости химических реакций при температурах Т1 и Т2;
g – температурный коэффициент (коэффициент Вант-Гоффа), определяется экспериментально.

44 (7) .Правило Вант-Гоффа.Правило Вант-Гоффа — эмпирическое правило, позволяющее в первом приближении оценить влияние температуры на скорость химической реакции в небольшом температурном интервале (обычно от 0 °C до 100 °C). Я. Х. Вант-Гофф на основании множества экспериментов сформулировал следующее правило:
При повышении температуры на каждые 10 градусов константа скорости гомогенной элементарной реакции увеличивается в два—четыре раза.
Уравнение, которое описывает это правило, следующее: 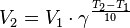где V₂— скорость реакции при температуре T₂ , V₁ — скорость реакции при температуре T₁, Y — температурный коэффициент реакции (если он равен 2, например, то скорость реакции будет увеличиваться в 2 раза при повышении температуры на 10 градусов).
Следует помнить, что правило Вант-Гоффа применимо только для реакций с энергией активации 60-120 кДж/моль в температурном диапазоне 10-400 oC. Правилу Вант-Гоффа также не подчиняются реакции, в которых принимают участие громоздкие молекулы, например, белки в биологических системах. Температурную зависимость скорости реакции более корректно описывает уравнение Аррениуса. Из уравнения Вант-Гоффа температурный коэффициент вычисляется по формуле: .

45 (8).Уравнение Аррениуса. Уравне́ние Арре́ниуса устанавливает зависимость константы скорости ~k химической реакции от температуры ~T.
Согласно простой модели столкновений, химическая реакция между двумя исходными веществами может происходить только в результате столкновения молекул этих веществ. Но не каждое столкновение ведёт к химической реакции. Необходимо преодолеть определённый энергетический барьер, чтобы молекулы начали друг с другом реагировать. То есть молекулы должны обладать некой минимальной энергией (энергия активации E_А), чтобы этот барьер преодолеть. Из распределения Больцмана для кинетической энергии молекул известно, что число молекул, обладающих энергией E>E_А , пропорционально 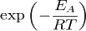. В результате скорость химической реакции представляется уравнением, которое было получено шведским химиком Сванте Аррениусом из термодинамических соображений: 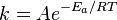. Здесь А характеризует частоту столкновений реагирующих молекул, R — универсальная газовая постоянная. В рамках теории активных соударений A зависит от температуры, но эта зависимость достаточно медленная: 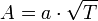. Оценки этого параметра показывают, что изменение температуры в диапазоне от 200 °C до 300 °C приводит к изменению частоты столкновений А на 10 %. В рамках теории активированного комплекса получаются другие зависимости А от температуры, но во всех случаях более слабые, чем экспонента. Уравнение Аррениуса стало одним из основных уравнений химической кинетики, а энергия активации — важной количественной характеристикой реакционной способности веществ.

46 (9).Энергия активации, ее определение.Сильное изменение скорости реакции с изменением температуры объясняет теория активации. Согласно этой теории в хими­ческое взаимодействие вступают только активные молеку­лы (частицы), обладающие энергией, достаточной для осущест­вления данной реакции. Неактивные частицы можно сделать активными, если сообщить им необходимую дополнительную энергию, - этот процесс называется активацией. Один из способов активации - увели­чение температуры: при повышении температуры число активных частиц сильно возрастает, благодаря чему резко увеличивается ско­рость. Энергия, которую надо сообщить молекулам (частицам) реагирующих веществ, чтобы превратить их в активные, называется энергией активации. Ее определяют опытным путем, обозначают буквой Е_a и обычно выражают в кДж/моль. Так, например, для соединения водорода и иода (Н₂ + I₂ = 2НI) Е_а = 167,4 кДж/моль, а для распада иодоводорода (2НI = Н₂ + I₂) Е_а = 186,2 кДж/моль. Энергия активации Е_a зависит от природы реагирующих веществ и служит характеристикой каждой реакции. Эти представления поясня­ются рисунком: на примере реакции в общем виде А₂ + В₂ = 2АВ. Ось ординат характеризует потенциаль­ную энергию системы, ось абсцисс - ход реакции: исходное состояние → переходное состояние → конеч­ное состояние. Чтобы реагирующие вещества А₂ и В₂ образовали про­дукт реакции АВ, они должны преодолеть энергетический барьер С. На это затрачивается энергия активации Е_а, на значение которой возрастает энергия систе­мы. При этом в ходе реакции из частиц реагирующих веществ обра­зуется промежуточная неустойчи­вая группировка, называемая переходным состоянием или активиро­ванным комплексом (в точке С), последующий распад которого приводит к образованию конечного продукта АВ. Механизм реакции можно изобразить схемой 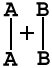.Если при распаде активированного комплекса выделяется больше энергии, чем это необходимо для активации частиц, то реакция экзо­термическая. Примером эндотермической реакции служит обратный процесс - образование из вещества АВ веществ А₂ и В₂: 2АВ = А₂ + В₂. В этом случае процесс протекает также через образование активированного комплекса А₂В₂, однако энергия активации больше, чем для прямого процесса: Е_а = Е_а + ∆H (∆H - тепловой эффект реакции). Для протекания эндотермических реакций требуется подвод энергии извне. Как видно из рисунка разность энергий конечного состояния систе­мы (H_кон) и начального (H_нач) равна тепловому эффекту реакции: ∆H = H_кон - H_нач. Скорость реакции непосредственно зависит от значения энергии активации: если оно мало, то за определенное время протекания реак­ции энергетический барьер преодолеет большое число частиц и скорость реакции будет высокой, но если энергия активации велика, то реакция идет медленно. При взаимодействии ионов энергия активации очень мала и ионные реакции протекают с очень большой скоростью (практически мгновенно).

47 (10).Основные понятия теории активных столкновений и теории переходного состояния .Одной из первых теорий, объясняющей механизм химических реакций была теория активных столкновений. Эта теория считала, что химическая реакция является результатом столкновения взаимодействующих частиц. Шведский физико-химик Сванте Аррениус предположил, что взаимодействуют лишь частицы, обладающие избыточной энергией.
Аррениус вывел закономерность, по которой скорость химической реакции зависит от температуры в виде следующего уравнения: W = A^.exp[-E/(RT)], где А - множитель, отражающий количество соударений реагентов (активных столкновений), которое приводит к химической реакции между ними.
В реакцию вступают не все частицы системы, а лишь те, которые обладают некоторой избыточной энергией, по сравнению со средней энергией остальных частиц. В противном случае все реакции протекали бы со взрывом. Аррениус назвал эту избыточную энергию - энергией активации.
Максвелл (в 1859 году) и Больцман (в 1869-71) открыли одну из важнейших закономерностей молекулярной физики и физики вообще, связав энергию молекулы с температурой N_E = N₀^.exp[-E/(RT)], где N_E - доля молекул с энергией E, N₀ - общее количество молекул в изучаемой системе, T - температура, R - универсальная газовая постоянная. Закон Максвелла-Больцмана показывает распределение молекул по энергиям их движения в идеальном газе. Он был выведен теоретически и подтвержден большим количеством экспериментов. Таким образом, экспериментально найденная зависимость скорости реакции от температуры была подтверждена законом распределения молекул по энергиям. Это удивительное совпадение и логическое объяснение одного итого же явления двумя независимыми науками выдвинуло теорию активных столкновений в ранг классических научных теорий. Основа теории активных столкновений:
Для того чтобы произошла химическая реакция, молекулы реагентов должны:
1) столкнуться;
2) обладать достаточной энергией - энергией активации;
3) иметь благоприятную ориентацию для скорейшего взаимодействия друг с другом. Энергии активации по ТАС должна по своему значению быть близкой к энергии связи в молекуле, которая разрушается в ходе химической реакции. Так и получилось в первых кинетических экспериментах, образцом здесь стала реакция взаимодействия газообразных йода и водорода. Однако во многих других газофазных реакциях этого не наблюдалось.
Стали учитывать не только поступательную, но и вращательную, а также колебательную составляющую энергии молекулы. Но в большинстве случаев и здесь результаты расчета и эксперимента серьезно расходились. Таким образом, теория активных столкновений установила связь между скоростью химической реакции, размером молекул, энергией их поступательного движения, частотой столкновений, но не объясняет, почему энергия молекулы, необходимая для вступления в реакцию (энергия активации), обычно намного меньше энергии химической связи, которую нужно разорвать, для того чтобы реакция произошла. Суть теории переходного состояния (активированного комплекса):1) частицы реагентов при взаимодействии теряют свою кинетическую энергию, которая превращается в потенциальную, и для того чтобы реакция свершилась, необходимо преодолеть некий барьер потенциальной энергии;
2) разница между потенциальной энергией частиц и упомянутым энергетическим барьером и есть энергия активации;
3) переходное состояние находится в равновесии с реагентами;
4) в тех реакциях, где энергия активации существенно ниже энергии разрыва химических связей, процессы образования новых связей и разрушения старых связей могут полностью или частично совпадать по времени.

Время существования активированного комплекса равно периоду колебания одной молекулы ( 10^-13 с), поэтому он не может быть обнаружен экспериментально и, соответственно, его нельзя выделить и изучить. Следовательно, доказать истинность теории переходного состояния можно только с помощью расчетов. И для этой цели ученые задействовали самую передовую на тот момент методику, которая тогда переживала бурный расцвет - квантовую химию. Выделилось даже целое направление в квантовой химии по расчетам энергии переходного состояния.

48 (11).Энергетическая диаграмма реакции. В качестве абсциссы в этих диаграммах используется так называемая координата реакции. Она является сложной функцией межатомных расстояний. Но для практических целей и простых молекул можно считать, что она характеризует изменения в межатомных расстояниях, которые происходят при сближении исходных молекул, образующих активированный комплекс, и взаимном удалении продуктов реакции при распаде активированного комплекса. По оси ординат откладывается потенциальная энергия всей системы.

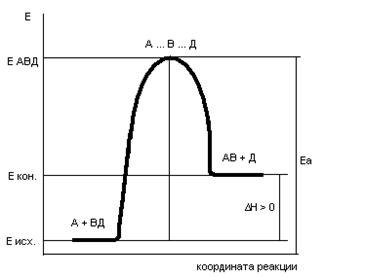∆Н < 0 , То дополнительное количество энергии, которое надо добавить к средней энергии молекул исходных веществ, чтобы соударение между молекулами исходных веществ было активным, называется энергией активации (Еа).
Энергия активации ощутимо влияет на значение константы скорости реакции и ее зависимости от температуры: чем больше Еа, тем меньше константа скорости и тем значительнее влияет на нее изменение температуры. 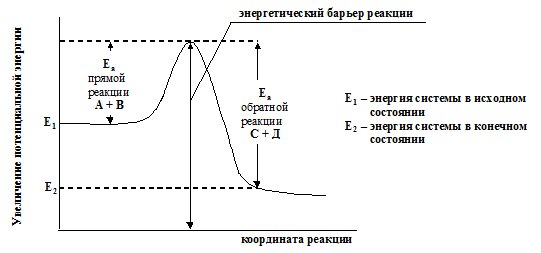Энергетическая диаграмма реакции А + В = С + Д

Константа скорости реакции связана с энергией активации сложной зависимостью, описанной уравнением Аррениуса: k=A× Е^-Еа/RT (18) ,где А – предэкспоненциальный множитель; Еа – энергия активации, R – универсальная газовая постоянная, равная 8,31 дж/моль–1К–1; Т – абсолютная температура; е – основание натуральных логарифмов.