Взаимосвязь между различными константами равновесия.

Найдем связь между k_p и k_C, гомогенной реакции, протекающей в газообразной фазе. Воспользуемся уравнением Клайперона-Менделеева:

Но по определению мольной объемной концентрации:

k_p - не является функцией давления. Из этого следует, что и k_C для идеальных газов также не является функцией давления. k_C≠ƒ(p).

Аналогичным образом можно установить взаимосвязь между другими константами, например между k_p и k_C. Для этого воспользуемся уравнением Дальтона:

p_i=p_общ*x₁.

Используя это соотношение получим:

Вывод: поскольку k_р≠ƒ(p), то из этого выражения следует, что k_x - зависит от давления в общем случае.

Из представленных выражений вытекает, что для реакций, которые проходят без изменений числа молей имеет место равенство:

k_p=k_x=k_C.

В этом случае величина константы является безразмерной величиной. В реальных системах, в случае широкого интервала изменяется давление и концентрации для реагируемых веществ, закон действующих масс нарушается, т.к. в газообразных, жидких и твердых системах, не является идеальными, всегда существует взаимодействие между молекулами. Поэтому и давление и концентрации не выражают действующих масс и константа равновесия не сохраняет постоянное значение. Обычно интервал изменения давлений, в котором еще можно пользоваться парциальным давлениями, а не фугитивными , не превышает 30-50 атм. Для ионных растворов трудно определить предел в котором соблюдается постоянство константы равновесия. Можно только отметить, что для растворов не электролитов, интервал в котором константы постоянны являются более широким. Эти отклонения связаны со сложными взаимосвязями в растворах между молекулами растворенного вещества и среднего растворителя.

29. Равновесие в газовой фазе

В качестве второго примера системы с переменным числом: частиц рассмотрим равновесие в системе, в которой протекает химическая реакция.

Предположим для конкретности, что в ходе химической ре­акции происходит соединение молекул А и В с образованием молекулы АВ. Молекула АВ в свою очередь распадается на от­дельные молекулы Лий. Оба процесса, соединения и распада, происходят с некоторой скоростью, под которой понимают чис­ло актов, происходящих в единицу времени. Скорости прямого процесса А-\-В—*АВ и обратного процесса АВ~*А+В, во­обще говоря, не равны друг другу. Поэтому химическая реак­ция идет преимущественно в одну сторону. Однако по про­шествии некоторого времени, когда произойдет накопление реагентов, возникающих в ходе более быстрой реакции, и умень­шение количества реагентов, исчезающих в ходе реакции, ско­рость быстрой реакции уменьшится, а скорость медленной реакции увеличится. В результате в системе установится неко­торое равновесное состояние. Число возникающих и распадаю­щихся молекул АВ будет одинаковым. В этом случае говорят о равновесной реакции А + В АВ. Удобнее записывать реак­цию в форме равенства. Если реакция происходит между не­сколькими веществами, то всякую химическую реакцию можно- записать в виде

= 0, (67,1>-

где gi — химические символы реагирующих веществ, a Vi — число реагирующих молей соответствующих веществ. При этом принято записывать реакции так, чтобы коэффициенты vs- для веществ, расходуемых в ходе реакции, имели отрицательный знак, а для образующих веществ — положительный. Например,, реакция образования паров воды из гремучей смеси

2На + 02 = 2Н20 должна с этой точки зрения записываться в виде 2Н20— 2Н2 — 02 = 0,

так что vIIi0 = 2, vHi= - 2, vCj= - 1.

Напишем условия химического равновесия в произвольной системе состоящей из исходных веществ и продуктов реакции..

Совокупности молекул исходного вещества и продуктов реакции можно считать некоторыми квазизамкнутыми системами, нахо­дящимися в термостате и слабо взаимодействующими между собой. Последнее условие выполнено, если число атомов, реа­гирующих в единицу времени, мало по сравнению с полным числом молекул в системе, что всегда выполнено в макроско­пической системе веществ при равновесной реакции.

Обычно приходится изучать равновесные состояния реаги­рующей системы при заданной температуре и давлении. Усло­вием равновесия поэтому служит требование

Ф(р, Т, ЛГ,) —min,

где Ni — число частиц данного сорта. При постоянных задан­ных значениях температуры и давления во всей системе усло­вие минимума можно переписать в виде

и, замечая, что изменение числа частиц данного сорта можно представить в виде

dN{ = VjfiW,

мы получаем условие равновесия в системе при наличии хи­мических реакций:

2v,n, = 0. (67,2)

При превращении одной молекулы первой подсистемы в одну молекулу второй подсистемы (случай, рассматривавшийся нами ранее), коэффициенты v,-, очевидно, равны vi = 1, = —1. В этом случае формула (67,2) оказывается тождественной с (61,4).

Мы видим, что химические равновесия определяются равен­ством парциальных потенциалов. Ввиду этого парциальные по­тенциалы часто называют химическими потенциалами.

31. Термодинамический вывод закона действующих масс

33.Влияние температуры и давления.

Символ +Q или -Q,записанный в конце термохимического уравнения, характеризует тепловой эффект прямой реакции.Он равен по величине тепловому эффекту обратной реакции, но противоположен ему по знаку.

Влияние температуры зависит от знака теплового эффекта реакции. При повышении температуры химическое равновесие смещается в направлении эндотермической реакции, при понижении температуры — в направлении экзотермической реакции. В общем же случае при изменении температуры химическое равновесие смещается в сторону процесса, знак изменения энтропии в котором совпадает со знаком изменения температуры. Зависимость константы равновесия от температуры в конденсированных системах описывается уравнением изобары Вант-Гоффа:

в системах с газовой фазой — уравнением изохоры Вант-Гоффа

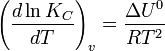
В небольшом диапазоне температур в конденсированных системах связь константы равновесия с температурой выражается следующим уравнением:

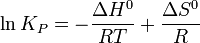
Например, в реакции синтеза аммиака

N₂ + 3H₂ ⇄ 2NH₃ + Q

тепловой эффект в стандартных условиях составляет +92 кДж/моль, реакция экзотермическая, поэтому повышение температуры приводит к смещению равновесия в сторону исходных веществ и уменьшению выхода продукта.

Давление существенно влияет на положение равновесия в реакциях с участием газообразных веществ, сопровождающихся изменением объёма за счёт изменения количества вещества при переходе от исходных веществ к продуктам:

При повышении давления равновесие сдвигается в направлении, в котором уменьшается суммарное количество молей газов и наоборот.

В реакции синтеза аммиака количество газов уменьшается вдвое: N₂ + 3H₂ ↔ 2NH₃

Значит, при повышении давления равновесие смещается в сторону образования NH₃, о чём свидетельствуют следующие данные для реакции синтеза аммиака при 400 °C:

34.Понятие о парциальных молярных величинах

В процессе образования раствора, например жидкого сплава цинка и кадмия, происходит изменение сил межатомного взаимодействия. Можно точно определить молярные объемы и 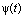, но объем раствора из-за изменения взаимодействий не равен сумме объемов компонентов. Чтобы избежать такой неопределенности, вводится понятие парциальных молярных величин для всех экстенсивных молярных величин (объем, энтальпия, энтропия, свободная энергия) . Пусть общее обозначение любой из них будет G. Для произвольного количества раствора данное свойство имеет значение G', а молярная величина — значение G;

где – число грамм-атомов компонентов раствора.

Добавим к произвольному количеству раствора бесконечно малое количество атомов или молекул компонента без изменения количества других компонентов и при постоянных Т и Р, тогда свойство G изменится на величину dG'. Отношение

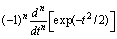
называют парциальной молярной величиной.

Парциальные молярные величины – это экстенсивные термодинамические свойства отдельных компонентов раствора. Физически они представляют собой ту долю от соответствующей величины, которая приходится на один грамм-атом или моль данного компонента раствора. В отличие от обычных соответствующий символ парциальных молярных величин снабжается звездочкой или черточкой

.

Введение парциальных молярных величин позволяет применять

к фазам переменного состава, т.е. к растворам, термодинамические уравнения, которые были выведены для веществ постоянного состава. Эти уравнения применимы к каждому отдельному компоненту раствора. Например, для веществ постоянного состава

для компонента раствора

35. Химический потенциал

Хими́ческий потенциа́л — термодинамическая функция, применяемая при описании состояния систем с переменным числом частиц. Определяет изменение термодинамических потенциалов (энергии Гиббса, внутренней энергии, энтальпии и т. д.) при изменении числа частиц в системе. Представляет собой энергию добавления одной частицы в систему без совершения работы. Применяется для описания материального взаимодействия. Определение химического потенциала можно записать в виде:

где Е — энергия системы, S — её энтропия, N — количество частиц в системе.

Эта формула определяет, кроме химического потенциала , также давление P и температуру T.

Для систем, состоящих из одного компонента, можно доказать, что химический потенциал задаётся формулой

,

где — потенциал Гиббса.

Если энергия системы зависит не от объёма, а от других термодинамических параметров , исходная формула принимает вид

Если в системе имеется несколько разных типов частиц, есть столько же разных химических потенциалов. Связь химического потенциала со свободной энергией называется Большим термодинамическим потенциалом.

Химический потенциал может быть определен по массе вещества, его количеству, либо числу частиц. Соответственно, в зависимости от величины по которой берется производная от энергии Гиббса, химический потенциал называется удельным (Дж/кг), молярным (Дж/моль) и химическим потенциалом, отнесенным к одной частице (Дж).

36. Общие условия достижения равновесия