
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Самопроизвольные процессы, энтропия химических систем
Процессы, протекающие без подвода энергии от внешнего источника, называются самопроизвольными. Самопроизвольно протекает большинство экзотермических реакций ( 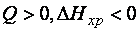 ): реакции горения, образования ржавчины на металле, взаимодействия активных металлов с растворами кислот и водой и пр. Но существуют самопроизвольные и эндотермические процессы, например, растворение некоторых солей в воде. Следовательно, кроме энтальпийного фактора (
): реакции горения, образования ржавчины на металле, взаимодействия активных металлов с растворами кислот и водой и пр. Но существуют самопроизвольные и эндотермические процессы, например, растворение некоторых солей в воде. Следовательно, кроме энтальпийного фактора (  ) имеется другая движущая сила самопроизвольных процессов.
) имеется другая движущая сила самопроизвольных процессов.
Рассмотрим пример. Имеется изолированный от окружающей среды сосуд с перегородкой, которая разделила его на две равные части. В одной половине сосуда инертный газ – аргон (Ar), в другой – инертный газ (He) (рис. 34). Концентрации газов, давление и температура одинаковы.

Рис. 34. Самопроизвольный переход системы к большему беспорядку
Удалим перегородку в сосуде, энергетическое состояние системы не изменится, однако газы перемешаются, т. е. система самопроизвольно перейдёт из состояния 1 в состояние 2.
Степень беспорядка в состоянии 1 < Степень беспорядка в состоянии 2;
Вероятность существования сост. 1 (W1) < Вероятность существования сост. 2 (W2).
Под термодинамической вероятностью существования системы 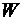 понимается, каким числом микросостояний системы можно описать данное макросостояние. При температуре абсолютного нуля (–273 °С) макросостояние системы описывается только одним микросостоянием, так как движение частиц при абсолютном нуле отсутствует. С повышением температуры число микросостояний системы увеличивается, так как усиливается движение микрочастиц.
понимается, каким числом микросостояний системы можно описать данное макросостояние. При температуре абсолютного нуля (–273 °С) макросостояние системы описывается только одним микросостоянием, так как движение частиц при абсолютном нуле отсутствует. С повышением температуры число микросостояний системы увеличивается, так как усиливается движение микрочастиц.
Следовательно, в изолированной системе самопроизвольно протекают процессы в направлении большего беспорядка или наиболее вероятного существования.
Энтропией системы называется логарифм термодинамической вероятности существования системы:
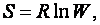 (29)
(29)
где 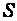 – энтропия системы, Дж/моль·К;
– энтропия системы, Дж/моль·К;  – молярная Const, Дж/моль·К,
– молярная Const, Дж/моль·К, 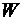 – термодинамическая вероятность системы.
– термодинамическая вероятность системы.
Энтропия 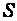 – количественная мера беспорядка в системе, чем выше энтропия, тем больше беспорядок, поэтому
– количественная мера беспорядка в системе, чем выше энтропия, тем больше беспорядок, поэтому 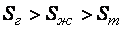 .
.
Энтропия вещества в стандартных условиях называется стандартной энтропией  , [Дж/моль∙ К]. В отличие от других термодинамических функций можно определить не только изменение энтропии
, [Дж/моль∙ К]. В отличие от других термодинамических функций можно определить не только изменение энтропии 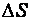 , но и её абсолютное значение. Энтропия простого вещества не равна нулю (см. приложение, табл. 6).
, но и её абсолютное значение. Энтропия простого вещества не равна нулю (см. приложение, табл. 6).
Изменение энтропии 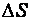 при самопроизвольном переходе системы из состояния 1 в состояние 2 (см. рис. 34) рассчитывается:
при самопроизвольном переходе системы из состояния 1 в состояние 2 (см. рис. 34) рассчитывается:
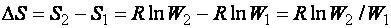 . (30)
. (30)
Так как  , то
, то 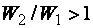 , а
, а 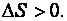
В изолированной системе самопроизвольно протекают процессы в направлении увеличения энтропии системы (  ) (второй закон термодинамики, определяет принципиальную возможность и направление протекания процесса).
) (второй закон термодинамики, определяет принципиальную возможность и направление протекания процесса).
Изменение энтропии химической реакции  равно сумме энтропий продуктов реакции за вычетом суммы энтропий исходных веществ с учетом стехиометрических коэффициентов.
равно сумме энтропий продуктов реакции за вычетом суммы энтропий исходных веществ с учетом стехиометрических коэффициентов.
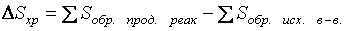 (31)
(31)
21) Термодинамические обратимые (квазистатические) и необратимые процессы.
Обратимые (квазистатические) и необратимые процессы.В процессе перехода из одного равновесного состояния в другое, который может происходить под влиянием различных внешних воздействий, система проходит через непрерывный ряд состояний, не являющихся, вообще говоря, равновесными. Для реализации процесса, приближающегося по своим свойствам к равновесному, необходимо, чтобы он протекал достаточно медленно. Но сама по себе медленность процесса ещё не является достаточным признаком его равновесности. Так, процесс разрядки компенсатора через большое сопротивление или дросселирование (см. Джоуля-Томсона эффект), при котором газ перетекает из одного сосуда в другой через пористую перегородку под влиянием перепада давлений, могут быть сколь угодно медленными и при этом существенно неравновесными процессами. Равновесный процесс, представляя собой непрерывную цепь равновесных состояний, является обратимым - его можно совершить в обратном направлении, и при этом в окружающей среде не останется никаких изменений. Т. даёт полное количественное описание обратимых процессов, а для необратимых процессов устанавливает лишь определённые неравенства и указывает направление их протекания.
22) Энергия Гиббса и энергия Гельмгольца как основные критерии направления самопроизвольных процессов и равновесия в неизолированных системах, мера химического сродства.
Изменение энтропии однозначно определяет направление и предел самопроизвольного протекания процесса лишь для наиболее простых систем – изолированных. На практике же большей частью приходится иметь дело с системами, взаимодействующими с окружающей средой. Для характеристики процессов, протекающих в закрытых системах, были введены новые термодинамические функции состояния: изобарно-изотермический потенциал (свободная энергия Гиббса) и изохорно-изотермический потенциал (свободная энергияГельмгольца).
Поведение всякой термодинамической системы в общем случае определяется одновременным действием двух факторов – энтальпийного, отражающего стремление системы к минимуму тепловой энергии, и энтропийного, отражающего противоположную тенденцию – стремление системы к максимальной неупорядоченности. Если для изолированных систем (ΔН = 0) направление и предел самопроизвольного протекания процесса однозначно определяется величиной изменения энтропии системы ΔS, а для систем, находящихся при температурах, близких к абсолютному нулю (S = 0 либо S = const) критерием направленности самопроизвольного процесса является изменение энтальпии ΔН, то для закрытых систем при температурах, не равных нулю, необходимо одновременно учитывать оба фактора. Направление и предел самопроизвольного протекания процесса в любых системах определяет более общий принцип минимума свободной энергии:
Самопроизвольно могут протекать только те процессы, которые приводят к понижению свободной энергии системы; система приходит в состояние равновесия, когда свободная энергия достигает минимального значения.
Для закрытых систем, находящихся в изобарно-изотермических либо изохорно-изотермических условиях свободная энергия принимает вид изобарно-изотермического либо изохорно-изотермического потенциалов (т.н. свободная энергия Гиббса и Гельмгольца соответственно). Данные функции называют иногда просто термодинамическими потенциалами, что не вполне строго, поскольку термодинамическими потенциалами являются также внутренняя энергия (изохорно-изэнтропный) и энтальпия (изобарно-изэнтропный потенциал).
Рассмотрим закрытую систему, в которой осуществляется равновесный процесс при постоянных температуре и объеме. Выразим работу данного процесса, которую обозначим Amax (поскольку работа процесса, проводимого равновесно, максимальна), из уравнений (I.53, I.54):
 (I.68)
(I.68)
 (I.69)
(I.69)
Преобразуем выражение (I.69), сгруппировав члены с одинаковыми индексами:
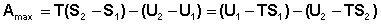 (I.70)
(I.70)
Введя обозначение:
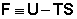 (I.71)
(I.71)
получаем:
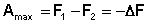 (I.72)
(I.72)
 (I.73)
(I.73)
Функция 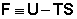 есть изохорно-изотермический потенциал (свободная энергия Гельмгольца), определяющий направление и предел самопроизвольного протекания процесса в закрытой системе, находящейся в изохорно-изотермических условиях.
есть изохорно-изотермический потенциал (свободная энергия Гельмгольца), определяющий направление и предел самопроизвольного протекания процесса в закрытой системе, находящейся в изохорно-изотермических условиях.
Закрытую систему, находящуюся в изобарно-изотермических условиях, характеризуетизобарно-изотермический потенциал G:
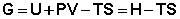 (I.74)
(I.74)
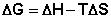 (I.75)
(I.75)
Поскольку –ΔF = Amax, можно записать:
 (I.76)
(I.76)
Величину А'max называют максимальной полезной работой (максимальная работа за вычетом работы расширения). Основываясь на принципе минимума свободной энергии, можно сформулировать условия самопроизвольного протекания процесса в закрытых системах.
Условия самопроизвольного протекания процессов в закрытых системах:
Изобарно-изотермические (P = const, T = const):
ΔG<0, dG<0
ΔF<0, dF< 0
Процессы, которые сопровождаются увеличением термодинамических потенциалов, протекают лишь при совершении работы извне над системой. В химии наиболее часто используется изобарно-изотермический потенциал, поскольку большинство химических (и биологических) процессов происходят при постоянном давлении. Для химических процессов величину ΔG можно рассчитать, зная ΔH и ΔS процесса, по уравнению (I.75), либо пользуясь таблицами стандартных термодинамических потенциалов образования веществ ΔG°обр; в этом случае ΔG° реакции рассчитывается аналогично ΔН° по уравнению (I.77):
 (I.77)
(I.77)
Величина стандартного изменения изобарно-изотермического потенциала в ходе химической любой реакции ΔG°298 есть мера химического сродства исходных веществ. Основываясь на уравнении (I.75), можно оценить вклад энтальпийного и энтропийного факторов в величину ΔG и сделать некоторые обобщающие заключения о возможности самопроизвольного протекания химических процессов, основываясь на знаке величин ΔН и ΔS.
1. Экзотермические реакции; ΔH < 0.
а) Если ΔS > 0, то ΔG всегда отрицательно; экзотермические реакции, сопровождающиеся увеличением энтропии, всегда протекают самопроизвольно.
б) Если ΔS < 0, реакция будет идти самопроизвольно при ΔН > TΔS (низкие температуры).
2. Эндотермические реакции; ΔH > 0.
а) Если ΔS > 0, процесс будет самопроизвольным при ΔН < TΔS (высокие температуры).
б) Если ΔS < 0, то ΔG всегда положительно; самопроизвольное протекание эндотермических реакций, сопровождающихся уменьшением энтропии, невозможно.
23) Изменения энергии Гиббса в реакциях.
Рассмотрим экзотермическую реакцию:
СО + 2Н2=> СН3ОН - 93,5 кДж
Действие энтальпийного фактора обусловливает ее протекание в прямом направлении.
∆H <0 (процесс экзотермический)
Однако наибольшее значение энтропии достигается при полном разложении метанола на водород и оксид углерода, так как при этом число молекул газов возрастает втрое.
Вычислим изменение энтропии системы при прямой реакции.
Изменение энтропии в ходе химической реакции ( ΔS) равно сумме энтропий продуктов за вычетом суммы энтропии исходных веществ.
Таблица 3. Стандартные энтропии веществ-участников реакции
| Вещество | Стандартная энтропия, S0 Дж/моль·K |
| CO (газ) | 197,5 |
| H2(газ) | 130,5 |
| CH3OH (газ) | 240,1 |
ΔS° = 240,1 Дж/моль·K· 1 моль —(197,5 Дж/моль·K· 1 моль + 130,5 Дж/моль·K· 2 моль) = -218,4 Дж/К.
Отсюда, при синтезе метанола энтропия уменьшается.
Таким образом энтальпийный и энропийный факторы действуют в противоположных направлениях.
Для того чтобы учесть действие обоих факторов в термодинамике используется функция состояния системы - энергия Гиббса (G). Она применяется для изобарно-изотермических условий и связана с энтальпией и энтропией простым соотношением:
G = H - TS.
Изменение энергии Гиббса в ходе химической реакции:
∆G = ∆H - T∆S
Характер этого изменения позволяет судить о принципиальной возможности или невозможности осуществления процесса.
Дата добавления: 2015-01-29; просмотров: 2896; Мы поможем в написании вашей работы!; Нарушение авторских прав |