Изменчивость (вариабельность) качества. Биномиальное распределение. Гипергеометрическое распределение. Распределение Пуассона.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины м.б. конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.

Биномиальное распределение.

Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна p (следовательно, вероятность непоявления q=1-p). Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях.

Поставим перед собой задачу: найти закон распределения величины Х. для ее решения требуется определить возможные значения Х и их вероятности. Очевидно, событие А в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, …, либо n раз. Таким образом, возможные значения Х таковы: , , , …, . Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:

(*),

где k = 0,1, 2, …, n.

Эта формула является аналитическим выражением закона распределения.

Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным» потому, что правую часть равенства (*) можно рассматривать как общий член разложения бинома Ньютона:

Т.о., первый член разложения определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях; второй член определяет вероятность наступления события n-1 раз; последний член определяет вероятность того, что событие не появится ни разу.

Числовыми характеристиками распределения являются:

- мат.ожидание числа бракованных изделий в выборке, равное произведению объема выборки на вероятность брака в партии ;

- дисперсия числа бракованных изделий в выборке равна произведению объема выборки на вероятность бракованных изделий в партии и на вероятность годных изделий в партии .

Для доли бракованных изделий в выборке:

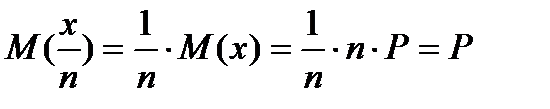
Математическое ожидание доли бракованных изделий практически невозможно определить.

Математическое ожидание отсчета получается при бесконечном повторении процедуры сравнения. С доверительной погрешностью ε заменяем , тогда правило принятия решения при контроле имеет вид:

;

- нормированная доля брака.

Объем выборки с возвратом определяем из формулы:

Вероятность P устанавливают либо по ранее полученным результатам контроля аналогичных партий изделий, либо принимают наибольшее значение произведения вероятностей.

Правило принятия решения можно представить в следующем виде:

;

-приемочное число

Часто требуется определить вероятность того, что число бракованных изделий в выборке не превышает x, такая вероятность называется накопленной или кумулятивной:

Для упрощения расчетов можно использовать соотношения вероятностей появления x и (x+1)-го бракованных изделий: