Гипергеометрический закон распределения.

Чаще встречается на практике выборка без возврата. Вероятность появления x бракованных изделий в выборке объемом n, взятой из партии объемом N, содержащей бракованных изделий , определяется по формуле:

Эта формула определяет распределение вероятностей, которое называют гипергеометрическим.

Числовыми характеристиками распределения являются: мат.ожидание и дисперсия.

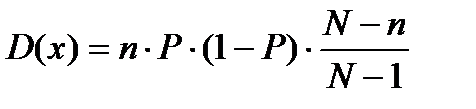
Для доли бракованных изделий в выборке:

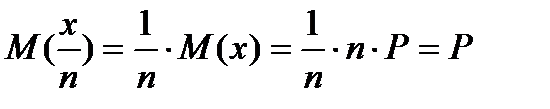
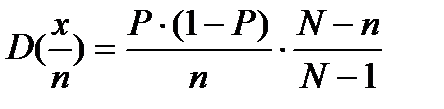
Необходимый объем выборки определяется из выражения:

;

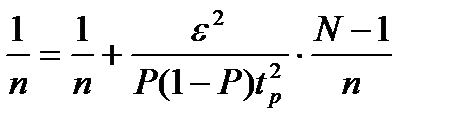
При больших объемах партий, первое слагаемое , а множитель , т.е. гипергеометрическое распределение, переходит в биномиальное. Для определение вероятности появления брака в выборке и кумулятивной вероятности

можно использовать соотношение:

В качестве модели выборочного контроля можно применять закон распределения вероятностей Пуассона:

Закон однопараметрический, имеет числовые характеристики:

Замена этим законом биномиального распределения допустима при небольших объемах выборок. Т.е. вероятность события очень мала( ).

При больших объемах выборок законом Пуассона заменяют гипергеометрическое распределение.

Гипергеометрическое распределение

Пусть в урне имеется N шаров, из которых M белые, а N-M чёрные. Выберем наугад из этой урны группу из n шаров (не возвращая вынутых шаров в урну и не интересуясь порядком шаров внутри группы). Обозначим через p_m,n вероятность того, что в рассматриваемой выборке будет ровно m белых шаров. Тогда можно записать

p_m,n= (1)

Случайная величина m может принимать значения от 0 до n. Распределение этой величины m называется гипергеометрическим, а уравнение (1) характеризует закон этого распределения. Гипергеометрическое распределение используется в теории статистического контроля качества – оно даёт распределение доли брака в выборке из контролируемой партии.

Гипергеометрическое распределение характеризуется тремя параметрами N, M и n (величина m является случайной переменной). Удобно в качестве параметров гипергеометрического распределения рассматривать N, n и

P= , (2)

где p – вероятность того, что первый вынутый шар будет белым. При этих параметрах математическое ожидание и дисперсия случайной величины m запишутся в таком виде:

M(m)=np, (3)

²(m)=npq (1- ), (4)

где q=1-p.

Рассмотрим такой случай, когда числа n и p фиксированы, а объём N совокупности неограниченно возрастает. Тогда из уравнений (3) и (4) следует, что математическое ожидание m будет оставаться неизменным, а дисперсия будет возрастать, стремясь к пределу, равному npq. При этом гипергеометрическое распределение стремится к биномиальному. Заметим, что при n 0,1N гипергеометрическое распределение становится уже настолько близким к биномиальному, что на практике можно пренебречь различием между двумя этими распределениями.

Биномиальное распределение

Пусть в урне имеется n₁ белых и n₂ чёрных шаров. Вероятность извлечения из урны белого шара p= , (1)

а вероятность извлечения чёрного шара

q= 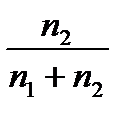. (2)

Очевидно, что имеет место соотношение

p+q=1. (3)

Проведём серию таких опытов: вынем из урны шар, запишем его цвет, положим его обратно в урну, перемешаем все шары, снова вынем шар и т.д. Возвращение шаров в урну нужно для того, чтобы вероятность извлечения белого шара (или чёрного) не изменялась от опыта к опыту.

Пусть в серии опытов мы проводим извлечение из урны n шаров. Обозначим через вероятность того, что ровно m из вынутых n шаров будут белыми (m n). Нетрудно вывести такое уравнение

p_m,n= p^mq^n-m= p^mq^n-m. (4)

Число m белых шаров в серии из n опытов является случайным. Это число m может принимать следующие значения:

0; 1; 2; 3; ….; n-1, n

с соответственными вероятностями

p_0,n p_1,n p_2,n … p_n,n.

Таким образом, уравнение (4) определяет собой распределение вероятностей случайного числа m, которое называется биномиальным.

Биномиальное распределение находит применение при статистическом контроле качества, в теории стрельбы и других областях.

Из уравнения (4) следует, например, что

p_0,n=qⁿ,

p_n,n=pⁿ. (5)

Вероятность того, что в серии из n опытов ни разу не появится белый шар, будет p_0,n. Вероятность того, что в серии из n опытов белый шар появится хотя бы один раз, будет очевидно, p’=1- p_0,n=1- qⁿ=1-(1-p)ⁿ. (6)

Математическое ожидание и дисперсия биномиального распределения запишутся в виде

M(m)=np ²(m)=npq. (8)

Если вместо случайной величины m рассматривать случайную частость

X= ,

то из уравнений (7) и (8) получим

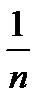
M(x)= M(m)=p, (x)= (m)= .

Функцию распределения запишем

F(m’)=Вер{m m’}= .

Как видно из уравнений (4) и (12), функция F(m’) зависит от трёх аргументов: m’, n и p. Поэтому составление таблиц для F(m’) является громоздким. Непосредственное вычисление F(m’) по уравнениям (4) и (12)является затруднительным при достаточно больших n и m’.

Однако здесь можно воспользоваться тем, что при n биномиальное распределение стремится к нормальному. Поэтому при больших n можно приближённо определить F(m’) при помощи нормального распределения, имеющего такие же математические ожидания и дисперсию, как и биномиальное распределение.

F(m’)=F₀ ( ).

Распределение Пуассона

Обозначим для краткости математическое ожидание . (1)

Рассмотрим частный случай. При m=2 получим

p_2,n= . (2)

При больших n и малых p из уравнения (2) приближённо имеем p_2,n= .

Действуя аналогичным образом, получаем для произвольного m . (3)

Уравнение (3) определяет собой распределение Пуассона (распределение редких событий). Этим уравнением можно пользоваться для случаев малых p, а для случая p, близких к единице, будет мало q=1-p, и тогда вместо уравнения (3) можно написать аналогичное уравнение , где b=nq=n (1-p).

Распределение Пуассона хорошо сходится с биномиальным распределением.

Распределение Пуассона имеет существенное преимущество для составления таблиц перед биномиальным распределением: в уравнение (3) входит только один параметр a=np, в то время как в уравнении 4 для биномиального распределения входят два параметра n и p.

Распределение Пуассона часто используется на практике как заменитель биномиального распределения. Кроме того, распределение Пуассона имеет самостоятельное значение. Справедливо следующее положение: если вероятность появления события в малом промежутке времени t пропорциональна t и события появляются независимо друг от друга, то число появлений события в течении данного промежутка времени распределяется по закону Пуассона. В силу этого положения распределение Пуассона широко применяется в теории надёжности и в теории массового обслуживания.

Указанное выше положение можно сформулировать в иной форме: если вероятность появления события на малой площади s пропорциональна s и события появляются независимо друг от друга, то число появлений события на данной площади распределяется по закону Пуассона.

Так, например, число осколков снаряда или ракеты, попадающих в цель, часто распределяется по закону Пуассона. В силу этого распределение Пуассона широко используется в теории стрельбы.

Для распределения Пуассона дисперсия равна математическому ожиданию:

.