А Классификация и общая характеристика основных методов контроля качества.

Статистические методы, применяемые для анализа состояния технологических процессов, могут быть разукрупнены на простейшие и классические. Их освоение следует начинать с применения «семи простых инструментов MQ», которые включают: контрольные листки, расслоение (стратификация), графики, диаграммы Парето, причинно-следственные диаграммы (диаграммы Исикавы или в другой транскрипции Ишикавы), гистограммы, диаграммы рассеивания (разброса), контрольные карты.

Все статистические методы базируются на имеющейся информации и понятии разброса. Применение каждого из этих методов должно начинаться со сбора необходимых данных. При этом необходимо четко сформулировать цель сбора интересующих нас сведений (анализ состояния технологических процессов, контроль, прогнозирование качества продукции), а также позаботиться об упорядочении получаемых данных, чтобы облегчить их последующую обработку. Сбор первичной информации рекомендуется вести с помощью контрольных листков. Собственно, контрольный листок не относится к «семи инструментам контроля качества». Заполнение контрольных листков является вспомогательным методом для использования гистограмм, диаграмм Парето, контрольных карт и т.п.

0. Контрольный листок — основная форма сбора первичных данных, их фиксации и упорядочения для дальнейшего использования.

Контрольные листки используются при проведении входного, текущего и выходного контроля материалов, деталей, узлов, блоков, готовой продукции; при анализе оборудования и технологических процессов, анализе брака и во многих других случаях. При этом формы листков могут быть самыми разнообразными и разрабатываются в зависимости от поставленной задачи с целью сбора конкретных данных, необходимых и достаточных для решения этой задачи.

При подготовке контрольных листков необходимо обращать внимание на следующее:

* способы заполнения контрольных листков должны быть предельно простыми (например, значки х, о, v или простые цифры);

* наглядность и полноту полученных данных;

* число пунктов проверки должно быть оптимальным (по возможности меньшим);

* форма контрольного листка должна быть простой, чтобы не затруднять заполнение, чтение, проверку, а также удобной для суммирования и анализа данных.

Контрольные листки составляют в строгом соответствии с поставленной целью так, чтобы на основе собранных данных можно было выработать правильную стратегию по улучшению работ; формы и методы применения контрольных листков должны постоянно совершенствоваться; исполнителей и всех лиц, которые заполняют контрольные листки, предварительно обучают и инструктируют, так как ошибки при заполнении листков влекут за собой ошибочные выводы.

Сущность статистической концепции заключается в том, что решения принимаются только на основе достоверных и корректных данных. Одним из наиболее простых и эффективных статистических методов, широко используемых для получения корректной информации, является метод расслоения. Говорят: «Без расслоения нет менеджмента качества».

1. Расслоение (стратификация) - инструмент, позволяющий произвести селекцию данных в соответствии с различными факторами.

Существуют различные методы расслоения, применение которых зависит от конкретных задач. Они применяются для выяснения действия отдельных причин на какую-либо величину или явление. В соответствии с этим методом производят расслоение данных, т.е. группируют данные в зависимости от условий их получения и производят обработку каждой группы данных в отдельности. Например, данные, относящиеся к изделию, изготовляемому в цехе на рабочем месте, могут в какой-то мере различаться в зависимости от исполнителя, технологических процессов, используемого оборудования, условий работы и т.д. Все эти отличия могут быть факторами расслоения. В производственных процессах часто используется метод 5М, учитывающий факторы, зависящие от человека (men), машины (machine), материала (material), метода (method), измерения (measurement).

Обычно при исследовании производственной проблемы расслоение осуществляется по следующим факторам:

* по исполнителям — по квалификации, полу, стажу работы и т.д.;

* расслоение по оборудованию и машинам — по новому и старому оборудованию, марке, конструкции, сроку службы и т.д.;

* материалу — по качеству сырья, партии, месту производства, сроку выпуска и т.д.;

* способу производства — технологическому приему, месту производства, условиям производства и т.д.;

* измерению — по методу измерения, типу измерительных средств или их точности и т.д.

Пусть одноименные детали изготовляются на нескольких станках. В этом случае всегда существует некоторая разница в технических данных этих станков, которая является причиной разброса характеристик производимых изделий. Поэтому можно получить ценную информацию о причинах дефектов, если анализировать не совокупные данные, а расслоенные по станкам, на которых были изготовлены детали. Влияние на разброс показателей качества деталей оказывают и другие факторы: квалификация и внимание исполнителей, качество исходных материалов, методы и условия производства, время изготовления и т.д. Проводя расслоение также и по этим факторам, можно значительно углубить анализ и повысить обоснованность заключений. Рассматривая каждый фактор, по которому проводится расслоение, можно выявить факторы второго порядка, оказывающие влияние на разброс показателей качества, зависящих от того или иного фактора первого порядка. Поэтому часто проводится расслоение еще и по факторам второго, а если окажется необходимым, то и третьего порядка.

Расслоение используется в случае применения других статистических методов: при построении причинно-следственных диаграмм; диаграмм Парето; гистограмм и контрольных карт.

2. График — инструмент, позволяющий наглядно представить, облегчить понимание смысла и выявить закономерности, которым подчиняется рассматриваемая группа данных.

График дает возможность не только оценить состояние на данный момент, но и спрогнозировать более отдаленный результат по тенденции (тренду) процесса, которую можно в нем обнаружить, а, следовательно, наметить меры, которые могут предупредить ухудшение состояния или улучшить положительный результат.

Различают следующие виды графиков:

* выраженный ломаной линией;

* столбчатый; круговой; ленточный; Z-образный;

* «радиационная» диаграмма;

* карта сравнения плановых и фактических показателей.

График, выраженный ломаной линией, применяется для выражения временных изменений, например, изменение с течением времени доли дефектных изделий или процент выхода годных изделий. По оси ординат на таком графике откладывают значение соответствующей величины, а по оси абсцисс — время. Нанесенные на график точки соединяют прямыми отрезками. Эффективность полученной информации возрастает, если при анализе данных расслоить их по таким факторам, как изделие, оборудование, участок и т.д. Пример такого графика для выражения изменения доли дефектных изделий по годам приведен на рис. 4.

Столбчатый график представляет количественную зависимость, выражаемую высотой столбика, таких факторов, как сумма потерь в результате брака от процесса, виды причины брака изделия и т.д. Разновидностями столбчатого графика являются гистограммы и диаграммы Парето. При построении столбчатого графика по оси ординат откладывают количество, по оси абсцисс - факторы; каждому фактору соответствует столбик. Примеры столбчатых графиков показаны на рис. 9—11.

Круговым графиком выражают соотношение составляющих какого-либо целого параметра и всего параметра в целом, например: соотношение типов деталей и общее число деталей; соотношение элементов, составляющих себестоимость изделия, и целое число, выражающее себестоимость и т.д. Целое принимается за 100% и выражается полным кругом. Составляющие выражаются в виде секторов круга и располагаются по кругу в направлении движения часовой стрелки, начиная с элемента, имеющего наибольший процент вклада в целое, в порядке уменьшения процента вклада. Последним ставится элемент «прочие». На круговом графике легко выделить сразу все составляющие и их соотношение. Пример кругового графика показан на рис. 5, где представлено соотношение распределений видов отказов изделий.

По графику, можно оценить соотношение составляющих видов отказов изделия. Если провести их расслоение, проанализировать причины и сравнить, по отдельным периодам, то можно получить информацию, которая позволит провести мероприятия по снижению вероятности отказов изделия.

Ленточный график используют для наглядного представления соотношения составляющих какого-либо параметра и одновременно для выражения изменения этих составляющих с течением времени, например: для представления причин отказов с течением времени и изменения их по месяцам.

При построении ленточного графика прямоугольник графика делят на зоны пропорционально составляющим или в соответствии с количественными значениями, и по длине ленты размечают участки в соответствии с соотношением составляющих по каждому фактору. Систематизируя ленточный график так, чтобы ленты располагались в последовательном временном порядке, можно оценить изменение составляющих с течением времени.

Z -образный график используют для оценки общей тенденции при регистрации по месяцам фактических данных, таких как число дефектных изделий, объем производства. объем сбыта и т.д.

График строится следующим образом: откладываются значения параметра (например, число дефектных изделий) по месяцам (за период одного года) с января по декабрь и соединяются отрезками прямой - получается график, образуемый ломаной линией; вычисляется кумулятивная сумма за конкретный месяц и строится соответствующий график; вычисляются итоговые значения, изменяющиеся от месяца к месяцу (меняется итог) и строится соответствующий график, образуемый ломаной линией. За меняющийся итог принимается в данном случае итог за год, предшествующий данному месяцу. Общий график, включающий три построенных указанным образом графика, имеет вид буквы 2, отчего он и получил свое название. По меняющемуся итогу можно определить тенденцию изменения за длительный период. Вместо меняющегося итога можно наносить на график планируемые значения и проверять условия достижения этих значений.

«Радиационная» диаграмма. Этот график строится следующим образом: из центра круга к окружности проводятся по числу факторов прямые линии (радиусы). На эти радиусы наносят деления градуировки и откладывают значения данных. Точки, которыми обозначены отложенные значения, соединяют отрезками прямой. Таким образом, «радиационная» диаграмма представляет собой комбинацию кругового и линейного графиков. Числовые значения, относящиеся к каждому из графиков, сравнивают со стандартными значениями и значениями, достигнутыми другими фирмами. Поскольку график отличается высокой наглядностью, его используют для анализа управления предприятием, оценки качества и т.д.

Карта сравнения плановых и фактических показателей. Карту нельзя отнести к графикам непосредственно, но это также метод визуализации данных. Она представляет собой таблицу, у которой по вертикали в две строки проставляются плановые и фактические достигнутые показатели, а по горизонтали — дата получения данных. Таблица наглядно показывает состояние выполнения плана. Такая карта применяется в случаях контроля распределения нагрузки на исполнителей или оборудование за определенный период, для оценки состояния выполнения работы за определенный период и т.д.

Таблица позволяет сравнить плановые и фактические показатели и вынести решение о степени отставания от плана. В случае отставания выясняется причина отставания и намечаются меры по ее устранению. Таблица может быть использована также для отдельных видов оборудования, отдельных операций, для тем мероприятий по повышению качества.

На промышленных предприятиях постоянно возникают всевозможные проблемы: появление брака, неполадки оборудования, задержка сроков поставок исходного сырья и материалов и т.д. Поиск решения этих проблем начинают с их классификации по отдельным факторам, сбора и анализа данных отдельно по группам проблем. Из анализа этих факторов часто обнаруживается, что в большинстве случаев большинство дефектов и связанных с ними потерь возникает из-за относительно небольшого числа причин, а материальных потерь на их долю приходится 70-80% (постулат Парето). Чтобы выяснить, какие из этих факторов являются основными, строят диаграмму Парето и проводят ее анализ.

3. Диаграмма Парето — инструмент, позволяющий объективно представить и выявить основные причины, влияющие на исследуемую проблему.

Диаграмма Парето позволяет установить основные факторы, с которых нужно начинать действовать с целью преодоления возникающих проблем.

Различают два вида диаграмм Парето: по результатам деятельности и по причинам.

Диаграмма Парето по результатам деятельности предназначена для выявления главной проблемы и отражает следующие нежелательные результаты деятельности:

* качество: несоответствия, ошибки, рекламации, ремонт, возвраты продукции;

* себестоимость: объем потерь, затраты;

* сроки поставок: нехватка запасов, ошибки в составлении счетов и срыв сроков поставок;

* безопасность: несчастные случаи, аварии.

Диаграмма Парето по причинам отражает причины проблем, возникающих в ходе производства, и используется для выявления главной из них:

* исполнитель работы: смена, бригада, возраст, опыт работы, квалификация, индивидуальные характеристики;

* оборудование: станки, агрегаты, инструменты, оснастка, организация использования, модели, штампы;

* сырье: изготовитель, вид сырья, партия;

* метод работы: условия производства, приемы работы, последовательность операций;

* измерения: точность, воспроизводимость, стабильность, тип измерительного прибора.

Построение диаграммы Парето состоит из следующих этапов.

Этап 1. Определите, какие проблемы необходимо исследовать и как собирать данные; как их классифицировать. Установите метод и период сбора данных.

Этап 2. Разработайте контрольный листок для регистрации данных с перечнем видов собираемой информации.

Этап 3. Заполните листок регистрации данных и подсчитайте итоги.

Этап 4. Разработайте бланк таблицы для проверок данных, предусмотрев в нем график для итогов по каждому проверенному признаку в отдельности, накопленной суммы числа дефектов, процентов к общему итогу и накопленных процентов (см. табл. 2).

При этом расположите данные, полученные по каждому признаку (фактору), в порядке значимости и заполните таблицу, учитывая, что группу «прочие» (в нашем случае код дефектов 8) всегда записывают в последнюю строку.

Этап 5. Начертите одну горизонтальную и две вертикальные оси.

Вертикальные оси: на левую ось нанесите шкалу с интервалом от 0 до числа, соответствующего общему итогу; на правую ось - шкалу с интервалами от 0 до 100%.

Горизонтальная ось — разделите ее на интервалы в соответствии с числом контролируемых признаков.

Этап 6. Постройте столбчатый график, где каждому виду брака соответствует прямоугольник (столбик), вертикальная строка которого соответствует значению суммы потерь от этого вида брака (основания всех прямоугольников равны).

Этап 7. Начертите кумулятивную кривую (кривую Парето). На вертикалях, соответствующих правым концам каждого интервала на горизонтальной оси, нанесите точки накопленных сумм (результатов или процентов) и соедините их между собой отрезками прямых.

Полученный график называется диаграммой Парето.

Этап 8. Нанесите на диаграмму все обозначения и надписи: надписи, касающиеся диаграммы (название, разметка числовых значений на осях, наименование контролируемого изделия, имя составителя диаграммы) и данных (период сбора информации, объект исследования и место его проведения, общее число объектов контроля).

Данные, представляемые в виде диаграммы Парето, нужны для корректной оценки состояния и разработки мероприятий по улучшению работы. Поэтому очень важно, чтобы таким анализом владели непосредственные исполнители - рабочие, контролеры, руководители производственных участков.

Качество изделий обеспечивается в процессе их изготовления и является результатом действия системы факторов и причин, составляющих процесс. При этом для производства изделий, качество которых удовлетворяло бы запросам потребителей, прежде всего, необходимо наиболее важным показателям качества (являющимся следствием) поставить в соответствие различные факторы производства (составляющие систему причинных факторов). Для этого важно хорошо понимать и контролировать зависимость между характеристиками качества и параметрами процесса. В этих случаях удобно использовать так называемую причинно-следственную диаграмму, которую часто называют диаграммой Исикавы или Ишикавы (по имени ее автора), диаграммой "причина-следствие", "рыбий скелет".

4. Причинно-следственная диаграмма - инструмент, позволяющий выявить отношение между показателями качества и воздействующими на них факторами.

С помощью причинно-следственной диаграммы можно решать широкий спектр конструкторских, технологических, организационных, экономических, социальных и других проблем. Изучаемая проблема условно изображается в виде прямой горизонтальной стрелки. Факторы, прямо или косвенно влияющие на проблему, изображаются наклонными стрелками, направленными к соответствующим следствиям. При поиске причин важно понимать, что характеристики, являющиеся следствием, обязательно испытывают разброс. Поиск среди этих причин факторов, оказывающих особенно большое влияние на разброс характеристик (т.е. результат), называют исследованием причин.

Алгоритм построения причинно-следственной диаграммы:

1. Выбор проблемы для решения («узкого места») — прямая горизонтальная стрелка.

2. Выявление наиболее существенных факторов, влияющих на проблему (причины первого порядка) — наклонные большие стрелки.

3. Раскрытие существенных факторов — выявление причин, влияющих на эти факторы (причины второго, третьего и последующих порядков) — маленькие наклонные стрелки.

4. Анализ и уточнение схемы: ранжирование факторов по их значимости; установление тех причин, которые в данный период времени поддаются корректировке.

5. Установление уровня, до которого должны быть доведены факторы, подлежащие корректировке.

6. Выявление производственных участков, отделов, конкретных лиц, ответственных за доведение корректируемых факторов до установленного уровня.

7. Разработка формы документа с целью слежения за корректируемыми факторами. Установление конкретных лиц, ответственных за достоверность информации.

8. Составление плана дальнейших действий — разработка мероприятий на перспективу. Установление ответственных лиц.

Определение причин, оказывающих наибольшее влияние на результаты, удобно производить по диаграмме Парето (см. п. 4). Часто применяют совместный анализ причинно-следственной диаграммы и диаграммы Парето.

В сложных случаях для выявления того, какие из причин наиболее важны, можно выяснить мнение участников анализа о ранжировании факторов, а затем с помощью диаграммы Парето выделить набравшие максимальное число голосов. При этом систематизацию причин следует проводить, рассматривая их в последовательности: от «маленьких стрелок» к «средним» и от «средних» к «большим».

Основу любого исследования (анализа) составляют данные, полученные в результате контроля и измерения одного или нескольких параметров изделий (информация о качестве). Во всех без исключения отраслях промышленности требуется проведение анализа точности и стабильности технологического процесса, осуществление наблюдений за качеством продукции и отслеживание различных показателей производства. Путем измерения параметров соответствующими средствами получают ряд данных, представляющих собой неупорядоченную последовательность значений параметра, на основе которых невозможно сделать корректные выводы. Поэтому для осмысления информации о качестве (статистических данных) часто строят гистограмму распределения.

5. Гистограмма - инструмент представления данных, сгруппированных по частоте попадания в определенный (заранее заданный) интервал.

Это столбиковая диаграмма, служащая для графического представления имеющейся количественной информации. При простоте построения гистограмма дает много полезной информации о разбросе качественных показателей, средних значениях, о точности и стабильности технологических процессов, о точностных возможностях технологического оборудования.

Гистограмма применяется главным образом для анализа значений измеряемых параметров, но может использоваться и для различных значений. Благодаря простоте построения и наглядности гистограммы нашли применение в самых разных областях.

Анализ гистограммы позволяет сделать заключение о состоянии процесса, однако если неясны условия контроля процесса или временные изменения, необходимо в комбинации с гистограммой использовать также контрольные карты и график, представляемый ломаной линией.

Поскольку гистограмма выражает условия процесса за период, в течение которого были получены данные, важную информацию может дать форма распределения гистограммы в сравнении с контрольными нормативами.

Различают следующие модификации формы гистограмм:

* с двусторонней симметрией (нормальное распределение). Гистограмма с таким распределением встречается чаще всего. Она указывает на стабильность процесса;

* вытянутая вправо — такую форму с плавно вытянутым вправо основанием гистограмма принимает в случае, когда невозможно получить значения ниже определенного, например, для диаметра деталей и т.д.;

* вытянутая влево — такую форму с плавно вытянутым влево основанием гистограмма принимает в случае, когда невозможно получить значения выше определенного;

* двугорбая - содержит два возвышения с провалом между ними и отражает случаи объединения двух распределений с разными средними значениями, например, в случае наличия разницы между двумя видами материалов, между двумя операторами и т.д. В этом случае можно провести расслоение по двум видам фактора, исследовать причины различия и принять соответствующие меры для его устранения;

* в форме обрыва, у которой как бы обрезан один край (или оба) — представляет случаи, когда, например, отобраны и исключены из партии все изделия с параметрами ниже контрольного норматива (или выше контрольного норматива, или те и другие);

* с отдельным островком — такой гистограммой выражаются случаи, когда была допущена ошибка при измерениях, когда наблюдались отклонения от нормы в ходе процесса и т. д. По результатам анализа гистограммы делают заключение о необходимости настройки измерительного прибора или срочного осуществления контроля параметров процесса и применяют соответствующие меры;

* не имеющая высокой центральной части — такая гистограмма получается в случаях, когда объединяются несколько распределений, в которых средние значения имеют небольшую разницу между собой. Анализ такой гистограммы целесообразно проводить, используя метод расслоения.

В тех случаях, когда известна норма, отмечают прямыми линиями верхнюю и нижнюю границы нормы (устанавливают контрольные нормативы) для сравнения с ними распределения, выраженного гистограммой. По гистограмме в этом случае сразу ясно, попадает ли гистограмма в интервал между контрольными нормативами. Если норму определить нельзя, на график наносят точки, отображающие запланированные значения, и проводят через них линии для сравнения с ними гистограммы. допущена ошибка при измерениях, когда наблюдались отклонения от нормы в ходе процесса и т.д. По результатам анализа гистограммы делают заключение о необходимости настройки измерительного прибора

В процессе исследования (анализа) часто приходится выяснять, существует ли зависимость между двумя различными параметрами процесса. Например, зависит ли качество собранного изделия от качества входных комплектующих деталей и узлов. Для выявления зависимости между показателями качества и основными факторами производства, а также корреляционной зависимости между факторами используют диаграммы разброса (рассеивания), которые также называют полем корреляции.

6. Диаграмма разброса (рассеивания) - инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных.

Диаграмма рассеивания дает возможность выдвинуть гипотезу о наличии или отсутствии корреляционной связи между двумя случайными величинами, которые могут относиться к характеристике качества и влияющему на нее фактору либо к двум различным характеристикам качества, либо к двум факторам, влияющим на одну характеристику качества.

При наличии корреляционной зависимости между двумя факторами значительно облегчается контроль процесса с технологической, временной и экономической точек зрения.

Построение диаграммы разброса выполняется в следующей последовательности.

1. Соберите парные данные (X, Y), между которыми вы хотите исследовать зависимость, и расположите их в таблицу. Желательно не менее 30 пар данных, так как в противном случае результаты анализа недостаточно достоверны.

2. Введите на плоскости систему координат 0ХY, причем шкалы на горизонтальной и вертикальной осях подбираются таким образом, чтобы обе длины рабочих частей получились примерно одинаковыми, тогда диаграмму будет легче читать. Возьмите на каждой оси от 3 до 10 градаций и используйте для облегчения чтения круглые числа.

3. Каждую пару данных отметьте на координатной плоскости точкой с координатами (X, Y). Если в разных наблюдениях получаются одинаковые значения, покажите эти точки либо рисуя концентрические кружки, либо нанося вторую точку вместе с первой.

4. Сделайте все необходимые обозначения: название диаграммы; интервал времени; число пар данных; названия и единицы измерения для каждой оси; данные о составителе диаграммы.

При наличии корреляционной зависимости можно осуществить контроль только одной (любой) из двух характеристик. При этом характер корреляционной зависимости, который определяется видом диаграммы разброса, дает представление о том, каким изменениям будет подвержен один из параметров при определенных изменениях другого. Так, при увеличении Х на диаграмме (рис. 13) Y также будет увеличиваться (прямая корреляция). В этом случае при осуществлении контроля за причинным фактором X характеристика Y будет оставаться стабильной.

На рис.14 показан пример обратной (отрицательной) корреляции. При увеличении X характеристика Y уменьшается. Если причинный фактор X находится под контролем, характеристика Y остается стабильной.

На рис.15 показан пример отсутствия корреляции, когда никакой выраженной зависимости между Х и Y не наблюдается. В этом случае необходимо продолжить поиск факторов, коррелирующих с Y, исключив из этого поиска фактор X.

Между параметрами Х и Y возможны также случаи криволинейной корреляции (рис.16). Если при этом диаграмму разброса можно разделить на участки, имеющие прямолинейный характер, проводят такое разделение и исследуют каждый участок в отдельности.

Существуют различные методы оценки степени корреляционной зависимости. Одним из них является метод вычисления коэффициента корреляции r по формуле

, (4)

где , —- значения параметров Х и Y для i-го измерения; , — средние арифметические значения величин Х и Y; п — число измерений в выборке (объем выборки).

Если r=±1, это свидетельствует о наличии корреляционной зависимости, если r=0, корреляционная зависимость отсутствует. Чем ближе коэффициент корреляции к единице, тем теснее зависимость между параметрами.

Более простым методом анализа степени корреляционной зависимости считается метод медиан, удобный при исследовании технологических процессов с использованием данных, полученных на рабочем месте.

На диаграмме разброса проводится вертикальная линия медианы и горизонтальная линия медианы. Выше и ниже горизонтальной медианы, справа и слева от вертикальной медианы будет равное число точек. Если число точек окажется нечетным, следует провести линию через центральную точку. В каждом из четырех квадрантов, получившихся в результате разделения диаграммы разброса вертикальной и горизонтальной медианами, подсчитывают число точек и обозначают , , , соответственно. Точки, через которые прошла медиана, не учитываются. Отдельно складывают точки в положительных и точки в отрицательных квадрантах:

Для определения наличия и степени корреляции но методу медианы используется специальная таблица кодовых значений, соответствующих различным k при двух значениях коэффициента риска 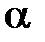(0,01 и 0,05).

Сравнивая меньшее из чисел и с кодовым значением, соответствующим значению k, делают заключение о наличии и характере корреляции. Если меньшее из чисел и оказывается равным или меньше табличного кодового значения, то корреляционная зависимость имеет место.

Погрешности производства вызывают неизбежное рассеивание и (или) устранимое рассеивание (разброс) показателей качества. Неизбежное рассеивание обусловлено изменениями качества сырья и материалов, а также изменениями в условиях производства - температуры, влажности воздуха, режимов резания и т.д. Устранимое рассеивание вызвано систематическими погрешностями производства: использование нестандартного сырья и материалов, нарушение технологического режима, недоработка технологической документации, неожиданная разладка оборудования, средств измерений и т.д. Для отражения изменений показателей качества во времени используют метод контрольных карт, который, в отличие от вышеописанных статистических методов, позволяет не только отслеживать состояние процесса во .времени, но и воздействовать на процесс до того, как он выйдет из-под контроля.

7. Контрольные карты — инструмент, позволяющий отслеживать ход протекания процесса и воздействовать на него, предупреждая его отклонения от предъявляемых к процессу требований.

Контрольная карта - графическое представление динамики процесса, состоящее из центральной линии, контрольных границ (границ регулирования) и конкретных значений имеющихся статистических данных, позволяющее оценить степень статистической управляемости процесса. Основные задачи, которые должны решать контрольные карты, следующие:

* давать информацию о том, находится ли процесс под статистическим контролем;

* четко показывать отклонения и сигнализировать о систематических дефектах;

* обеспечивать мероприятия по улучшению процесса.

Контрольные карты (КК) находят широкое применение при анализе и регулировании технологических процессов (ТП). Если точки, наносимые на КК, не выходят за границы регулирования, то ТП считают протекающим стабильно. Такое расположение точек расценивают как неизбежное рассеивание показателей качества, не требующее вмешательства в ход процесса. Если же точки на карте выходят за контрольные границы, то считается, что с ТП возникли какие-то систематические погрешности, которые должны быть выявлены и устранены. Контрольные карты являются источником полезной информации, так как помимо рассеивания показателей качества позволяют дать вероятностную оценку средних значений, т.е. уровня настройки ТП. Благодаря указанным свойствам карты являются одним из эффективных средств анализа и совершенствования ТП.

Основным видом по количественному признаку является контрольная карта ( -R). В тех случаях, когда показатели качества определяются качественными данными, например, степенью загрязнения или интенсивностью окрашивания, которые трудно выразить в количественном виде, обычно применяют контрольные карты по альтернативному признаку. Наибольшее распространение в практике отечественных и зарубежных предприятий получили p- карты, np- карты, с- карты, u- карты. Доля (процент) дефектных изделий (р),число бракованных изделий (пр) статистически описывается биноминальным законом распределения.

Карта- пр (карта числа дефектных изделий) строится аналогично и применяется в тех случаях, когда объем проверенных изделий п является постоянным (п=const).

Контрольные p- карты и np- карты строятся на основе биноминального распределения.

С- карта — карта контроля суммарного числа дефектов. В основе использования С- карты лежит распределение Пуассона и постоянство объема проверяемых изделий (и= const). В этом случае степень отклонения от требуемых норм можно выразить суммарным числом дефектов С, обнаруженных в проверяемых изделиях

U- карта (карта контроля числа дефектов на единицу продукции) может применяться при условии переменного числа проверяемых изделий п и является более информативной (по сравнению с С- картой), так как является конкретным показателем ТП, особенно когда речь идет об исправлении дефектов. Применение U- карты совместно с контрольным листком дает прекрасные результаты и позволяет существенно уменьшить дефектность, повысить стабильность и улучшить качество технологических процессов.

Планы выборочного контроля

Основное назначение

Общая проблема, с которой сталкиваются инженеры по контролю качества, состоит в том, чтобы определить, сколько изделий из партии (например, полученной от поставщика) необходимо исследовать, чтобы быть уверенными в том, что изделия этой партии обладают приемлемым качеством. Допустим, что у вашей автомобильной компании есть поставщик поршневых колец для небольших двигателей, и ваша цель – разработать процедуру выборочного контроля поршневых колец в присылаемых партиях, обеспечивающую требуемое качество. В принципе эта проблема сходна с проблемой, рассмотренной в разделе Контроль качества, где обсуждаются вопросы статистического контроля качества промышленной продукции.

Выборочный контроль при приемке. Процедуры выборочного контроля применяются в том случае, когда нужно решить, удовлетворяет ли определенным спецификациям партия изделий, не изучая при этом все изделия. В силу природы проблемы – принимать или не принимать партию изделий – эти методы иногда называют статистическим приемочным контролем

Преимущества над полным контролем. Очевидное преимущество выборочного контроля над полным (сплошным) контролем партии состоит в том, что изучение только выборки (а не всей партии) требует меньшего времени и финансовых затрат. В некоторых случаях исследование изделия является разрушающим (например, испытание стали на предельную прочность), и сплошной контроль уничтожил бы всю партию. Наконец, с точки зрения управления производством, отбраковка всей партии или поставки от данного поставщика (на основании выборочного контроля) вместо браковки лишь определенного процента дефектных изделий (на основании сплошного контроля) часто заставляет поставщиков строже придерживаться стандартов качества.