БИЛЕТ № 15

16. Понятие кольца многочленов над конечным полем. Неприводимые многочлены. Порядок многочленов над конечным полем. Число нормированных неприводимых многочленов степени n над конечным полем .

Неприводимый многочлен — многочлен, неразложимый на нетривиальные (неконстантные) многочлены. Неприводимые многочлены являются неприводимыми элементами кольца многочленов.

Определение

Неприводимый многочлен над полем ― многочлен от переменных над полем является простым элементом кольца , то есть, непредставим в виде произведения , где и ― многочлены с коэффициентами из , отличные от констант.

Многочлен называется абсолютно неприводимым, если он неприводим над алгебраическим замыканием поля коэффициентов. Абсолютно неприводимые многочлены одной переменной ― это многочлены 1-й степени и только они. В случае нескольких переменных существуют абсолютно неприводимые многочлены сколь угодно высокой степени — например, любой многочлен вида

абсолютно неприводим.

Свойства

- Кольцо многочленов факториально: любой многочлен разлагается в произведение неприводимых многочленов, причем это разложение определено однозначно с точностью до постоянных множителей.

- Над полем вещественных чисел любой неприводимый многочлен одной переменной имеет степень 1 или 2, причем многочлен 2-й степени неприводим тогда и только тогда, когда он имеет отрицательный дискриминант.

- Над любым полем алгебраических чисел существуют неприводимый многочлен сколь угодно высокой степени; например, многочлен , где и 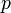― некоторое простое число, неприводим в силу критерия Эйзенштейна.

- Если 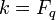— конечное поле из элементов, а — натуральное число, то существует хотя бы один неприводимый многочлен степени n из .

- Предположим ― целозамкнутое кольцо с полем частных (например и ) и ― многочлен одной переменной со старшим коэффициентом 1, тогда в , причем и имеют старший коэффициент 1, то .

- Редукционный критерий неприводимости. Пусть задано соотношение областей целостности Если степень многочлена совпадает со степенью многочлена 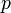и неприводим над полем частных области , то не существует разложения , где 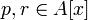и отличны от константы.

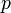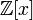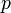- Например, многочлен со старшим коэффициентом 1 прост в (и, следовательно, неприводим в ), если прост многочлен , полученный из редукцией коэффициентов по модулю простого числа.

Примеры

Следующие пять многочленов демонстрируют некоторые элементарные свойства неприводимых многочленов:

Над кольцом целых чисел,первые два многочлена — приводимые, последние два — неприводимые. (Третий вообще не является многочленом над целыми числами).

Над полем рациональных чисел, первые три многочлена являются приводимыми, двое других — неприводимыми.

Над полем действительных чисел, первые четыре многочлена — приводимые, но является неприводимым. В поле действительных чисел неприводимыми являются линейные многочлены и квадратичные многочлены без действительных корней. Например разложение многочлена в поле действительных чисел имеет вид . Оба множителя в данном разложении являются неприводимыми многочленами.

Над полем комплексных чисел, все пять многочленов — приводимые. Фактически, каждый отличный от константы многочлен над может быть разложен на множители вида:

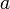где — степень многочлена, — старший коэффициент, — корни . Поэтому единственными неприводимыми многочленами над являются линейные многочлены (основная теорема алгебры).