КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Конечные поля
Многочлены с целочисленными коэффициентами, которые являются неприводимыми над полем 
могут быть приводимыми над конечным полем. Например, многочлен 
является неприводимым над , но над полем 
из двух элементов мы имеем: 
Кольцом R называется множество R с двумя бинарными операциями, обозначаемыми + или × такими, что:
1. R – абелева группа относительно операции + (т.е. выполняется коммутативный закон сложения a+b=b+a)
2. Операция × ассоциативна т.е. для любых a, b, c Î R ® (a × b) × c = a ×(b × c)
3. Выполняются законы дистрибутивности: " a, b, c Î R справедливо a × (b + c) = ab + ac; (b + c)× a = ba + ca.
Здесь операции + и × не обязательно являются обычным сложением и умножением. Единичный элемент аддитивной группы кольца K называется нулем и обозначается 0, а обратный к элементу a этой группы обозначают –a. Для кольца выполняются по определению свойства:
a × 0 = 0 × a = 0 длявсех a Î R
( -a) × b = a × ( -b) = -ab длявсех a,b Î R.
Кольцо называется кольцом с единицей, если оно имеет мультипликативную единицу, т.е. существует такой элемент e Î R, что a × e = e × a = a для всех "a Î R
Кольцо называется коммутативным, если операция × коммутативна a × b = b × a
Кольцо называетсяцелостным кольцом(или областью целостности), если оно является коммутативным кольцом с единицей e ¹ 0, в котором равенство a × b = 0 влечет за собой a=0 или b=0.
Кольцо R называетсятеломеслиR ¹ {0} и ненулевые элементы в R образуют группу относительно операции ×. Другими словами тело– это кольцо с единицей, в котором для каждого элемента a ¹ 0 существует обратный по умножению элемент a -1 такой, что a×(a -1)=1.
Полем называется тело, операция × в котором коммутативна, т.е. a×b = b×a
Поскольку основной алгебраической структурой, которая будет использоваться в дальнейшем, является поле, рассмотрим более подробно его определения.
Поле есть множество F на котором заданы две операции, называемые сложением + и умножением ×, и которое содержит два выделенных элемента 0 и е, причем 0 ¹ е. Поле это абелева группа по сложению, единичным элементом которой является 0, а элементы из F отличные от нуля, образуют абелеву группу по умножению, единичным элементом которой является е. Операции сложения и умножения в поле связаны законом дистрибутивности a(b+c)=ab+ac. Второй закон дистрибутивности (b+c)a=ba+ca выполняется автоматически в силу коммутативности операции умножения. Элемент 0 называется нулевым, а элемент е – единицей т.е. е=1.
Свойство поля, появляющееся из определения целостности кольца, т.е. равенство a×b=0 влечет a=0 или b=0, выражают словами «отсутствуют делители нуля». Другими словами в коммутативном кольце ненулевой элемент а называют делителем нуля, если существует другой ненулевой элемент b такой, что a×b=0. Если в кольце нет делителей нуля, то оно называется кольцом без делителей нуля или областью целостности. Никакой делитель нуля не может иметь обратного по умножению элемента. Поэтому никакое поле и тело не содержат делителей нуля.
Конечное поле - это поле содержащее конечное число элементов.
Многочлен f(x)ÎF[x] называется неприводимым над полем F или в кольце F[x], если он имеет положительную степень и равенство f(x)=g(x)×h(x); g(x),h(x)ÎF[x] может выполнятся лишь в том случае, когда либо g(x), либо h(x) являются постоянными многочленами (т.е. имеют степень 
и являются константами).
Неприводимость многочлена существенным образом зависит от того, над каким полем он рассматривается.
Примеры:
1. Многочлен f(x)=x2 -2 ÎQ неприводим над полем рациональный чисел Q, но приводим над полем действительных чисел R т.к. 
.
Определение. Пусть f(x)ÎFq[x] ненулевой многочлен. Если f(0)¹0, то наименьшее натуральное число е, для которого многочлен f(x) делит (xe -1) называется порядком многочлена f(x) и обозначается ord(f(x)). Если же f(0)=0, то многочлен f(x) однозначно представим в виде f(x)=xhg(x) где hÎN, g(x)ÎFq[x] и g(0)=0 и тогда ord(f(x)) многочлена f(x) определяется как ord(g(x)).
Порядок многочлена иногда называют его периодом или экспонентой многочлена. Порядок неприводимого многочлена можно определить, пользуясь следующей теоремой.
Теорема. Пусть f(x)ÎFq[x] неприводимый многочлен степени m, удовлетворяющий условию f(0)¹0. Порядок этого многочлена совпадает с порядком любого корня этого многочлена в мультипликативной группе F* поля Fqm.
Отсюда вытекает важное следствие: Если f(x)ÎFq[x] неприводимый многочлен степени m над полем Fq, то его порядок ord(f(x)) делит число qm -1.
Значения порядков многочленов играют важную роль при формировании линейных рекуррентных псевдослучайных последовательностей над конечными полями и кольцами, которые в свою очередь являются основой для создания поточных криптосистем.
Теорема. Для каждого конечного поля 
и каждого nÎN произведение всех нормированных неприводимых многочленов над , степень которых делит n, равно 
.
Следствие: Если 
число нормированных неприводимых многочленов из 
степени d, то 
для всех n, где суммирование берется по всем положительным делителем d числа n.
Из последнего выражения, используя арифметическую функцию Мебиуса можно получить точную формуле для числа нормированных неприводимых многочленов фиксированной степени из кольца 
.
Для nÎN функция Мебиуса m(n) удовлетворяет соотношению
.
Тогда существует теорема: Число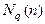 
нормированных неприводимых многочленов степени n в кольце 
равно
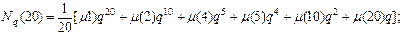
Для функции Мебиуса справедливо выражение
62. Парадигма доверия: значимость и причины возникновения уязвимостей, роль оценки. Представление требований доверия: структура класса, семейства, компонента, элемента. Примеры классов доверия. Парадигма поддержки доверия. Оценочные уровни доверия (ОУД1-ОУД7). Их примерное соответствие требованиям по классам безопасности Оранжевой книги, Европейских критериев и РД ГТК РФ.
Парадигма доверия
Цель данного подраздела состоит в изложении основных принципов и подходов к установлению доверия к безопасности. Данный подраздел позволит читателю понять логику построения требований доверия в настоящем стандарте.
Основные принципы ГОСТ Р ИСО/МЭК 15408 состоят в том, что следует четко сформулировать угрозы безопасности и положения политики безопасности организации, а достаточность предложенных мер безопасности должна быть продемонстрирована.
Более того, следует предпринять меры по уменьшению вероятности наличия уязвимостей, возможности их проявления (т. е. преднамеренного использования или непреднамеренной активизации), а также степени ущерба, который может явиться следствием проявления уязвимостей. Дополнительно следует предпринять меры для облегчения последующей идентификации уязвимостей, а также по их устранению, ослаблению и/или оповещению об их использовании или активизации.
Дата добавления: 2015-04-18; просмотров: 159; Мы поможем в написании вашей работы!; Нарушение авторских прав |