Марковский случайный процесс, уравнение Колмогорова. Стационарный марковский процесс, расчет надежности восстанавливаемых систем.

Процесс является марковским, если дальнейший ход процесса зависит от его состояния в момент t=0 и не зависит от предыстории процесса. Это условие выполняется, если времена безотказной работы и восстановления всех элементов подчиняются экспоненциальному закону.

Марковский процесс задается матрицей интенсивностей переходов l_ij(t) из i-го в j-е состояние

lij(t)= ,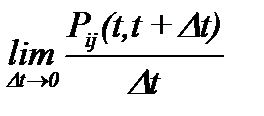

где Pij(t,t+Dt) - вероятность перехода из i-го в j-е состояние за время от момента t до t+Dt.

Если для всех состояний интенсивности переходов постоянны, не зависят от времени (lij=const), то марковский процесс называется однородным и матрица переходов имеет следующий вид:

l .

Для наглядного представления возможных переходов пользуются графом переходов, на котором узлами изображают состояния, а дугами возможные переходы, помечая их соответствующими значениями интенсивностей переходов

Интересующие нас показатели надежности системы могут быть найдены, если определена матрица-столбец P(t) вероятностей всех состояний

P(t) = ,

где Pk(t) - вероятность того, что в момент t процесс находится в состоянии k.

По формуле полной вероятности запишем выражение для вероятности Pk(t+Dt) застать процесс в состоянии k в момент времени t+Dt. Возможны два варианта:

- с вероятностью Pk(t) в момент t процесснаходился в этом состоянии и за время Dt не вышел из него в любое другое состояние j ( 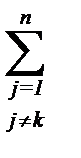lkjDt – вероятность противоположного события того, что за время Dt система уйдет из k-го состояния);

- с вероятностью Pi(t) в момент t процесснаходился в каком-либо состоянии i и за время Dt перешел в состояние k

Pk(t+Dt)=Pk(t) (1- lkjDt )+ Pi(t)likDt + o(Dt),

где o(Dt) - малые величины, более высокого порядка по сравнению с Dt, соответствующие двум или более переходам за времяDt.

Произведя элементарные преобразования, получим:

Перейдя к пределу

,

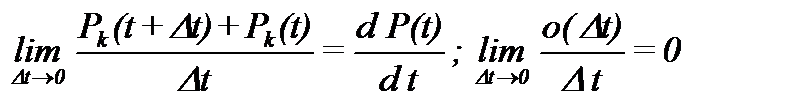получим систему n линейных дифференциальных уравнений с n неизвестными, называемых уравнениями Колмогорова:

Пребывание процесса в любой момент времени t в одном из состояний 1£k£n образует полную группу событий, поэтому

. (2.5)

Уравнения системы (2.4) линейно зависимы, поэтому их необходимо дополнить нормирующим условием (2.5), заменив этим условием любое из уравнений Колмогорова.

Начальными условиями для системы (2.4) является матрица-столбец P(0) вероятностей пребывания процесса в различных состояниях при t=0:

P(0) = (2.6)

При составлении уравнений Колмогорова по графу состояний пользуются следующими правилами:

1) в левой части равенства записывается производная вероятности рассматриваемого состояния;

2) в правой части уравнения стоит столько слагаемых, сколько дуг (стрелок) связывает данное состояние с другими состояниями;

3). каждое слагаемое представляет собой произведение вероятности состояния, из которого выходит дуга (стрелка) на интенсивности соответствующего перехода;

4) слагаемые, относящиеся к выходящим дугам (стрелкам), имеют знак минус, к входящим – плюс.