
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Стационарный Марковский случайный процесс.
Если число состояний системы конечно и из каждого состояния за конечное число шагов можно перейти в любое другое состояние, то существуют отличные от нуля и единицы предельные вероятности состояний, причем они не зависят от начального состояния системы:

Будем называть вероятность pk застать систему в состоянии k в произвольный достаточно удаленный от начала работы момент времени t стационарной вероятностью состояния k. Стационарный режим имеют только процессы, описывающие работу систем с восстановлением. Чтобы вычислить стационарные вероятности pk, достаточно в системе уравнений Колмогорова (2.4) все производные приравнять к нулю 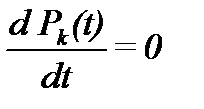 . При этом система дифференциальных уравнений превратится в систему линейных алгебраических уравнений, которая сравнительно легко решается даже при большой размерности.
. При этом система дифференциальных уравнений превратится в систему линейных алгебраических уравнений, которая сравнительно легко решается даже при большой размерности.
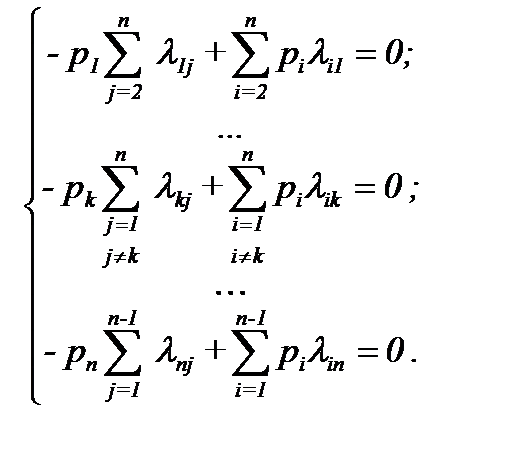 (2.8)
(2.8)
Нормирующее условие 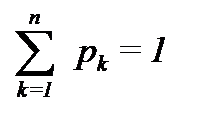 .Согласно эргодической теореме Хинчина стационарные вероятности pk при t®¥ сходятся по вероятности к средней доле времени пребывания системы в k-м состоянии. Следовательно, интересующие нас показатели надежности: коэффициент готовности kr и коэффициент простоя kп - можно вычислить по формулам:
.Согласно эргодической теореме Хинчина стационарные вероятности pk при t®¥ сходятся по вероятности к средней доле времени пребывания системы в k-м состоянии. Следовательно, интересующие нас показатели надежности: коэффициент готовности kr и коэффициент простоя kп - можно вычислить по формулам: 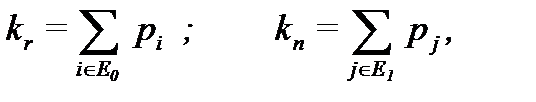
Дата добавления: 2015-04-18; просмотров: 311; Мы поможем в написании вашей работы!; Нарушение авторских прав |