
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Предел функции. Основные свойства предела.
Предел функции обозначается как 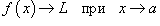 или через символ предела: или через символ предела: 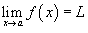 . Всюду ниже предполагается, что пределы функций . Всюду ниже предполагается, что пределы функций 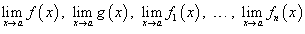 существуют.
Предел суммы
Предел суммы двух функций равен сумме пределов этих функций: существуют.
Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:
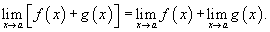 Расширенное правило суммы
Расширенное правило суммы
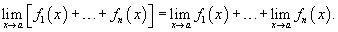 Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
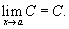 Предел произведения функции на постоянную величину
Постоянный коэффициент можно выносить за знак предела:
Предел произведения функции на постоянную величину
Постоянный коэффициент можно выносить за знак предела:
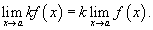 Предел произведения
Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):
Предел произведения
Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):
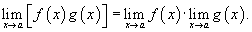 Расширенное правило произведения
Расширенное правило произведения
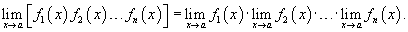 Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
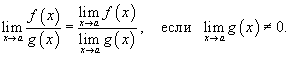 Предел степенной функции
Предел степенной функции
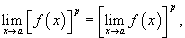 где степень p - действительное число. В частности,
где степень p - действительное число. В частности,
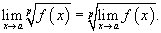 Если f ( x ) = x, то
Если f ( x ) = x, то
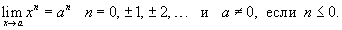 Предел показательной функции
Предел показательной функции
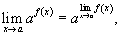 где основание a > 0.
Предел логарифмической функции
где основание a > 0.
Предел логарифмической функции
 где основание a > 0.
Теорема "о двух милиционерах"
Предположим, что
где основание a > 0.
Теорема "о двух милиционерах"
Предположим, что 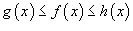 для всех x близких к a, за исключением, быть может, самой точкиx = a. Тогда, если для всех x близких к a, за исключением, быть может, самой точкиx = a. Тогда, если
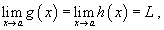 то
то
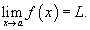 То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу L.
То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу L.
|
| Пример |
Найти предел 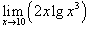 .
Решение. .
Решение.
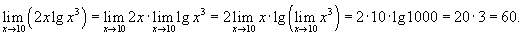
|
Дата добавления: 2015-04-18; просмотров: 303; Мы поможем в написании вашей работы!; Нарушение авторских прав |