Применение производной для нахождения промежутков монотонности функции. Экстремум функции.

Связь монотонности функции с ее производной

Теорема

(Об условии возрастания/убывания монотонной функции)

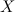Если производная функции на некотором промежутке , то функция возрастает на этом промежутке; если же 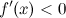на промежутке 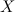, то функция убывает на этом промежутке.

Замечание

Обратное утверждение формулируется несколько иначе. Если функция возрастает на промежутке, то или не существует.

Пример

Задание. Исследовать функцию на монотонность на всей числовой прямой.

Решение. Найдем производную заданной функции:

Для любого действительного : , а поэтому делаем вывод, что заданная функция возрастает на всей действительной оси.

Ответ. Функция возрастает на всей действительной оси.

Понятие экстремума функции