Второе достаточное условие экстремума

Теорема

(Второе достаточное условие экстремума)

Пусть для функции выполнены следующие условия:

1. она непрерывна в окрестности точки ;

2. первая производная в точке ;

3. в точке .

Тогда в точке достигается экстремум, причем, если , то в точке функция имеет минимум; если , то в точке функция достигает максимум.

Пример

Задание. Исследовать функцию 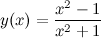на экстремум с помощью второй производной.

Решение. Находим первую производную заданной функции:

Находим точки, в которых первая производная равна нулю:

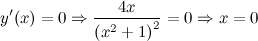
Вторая производная заданной функции:

В стационарной точке вторая производная , а значит, в этой точке функция достигает минимум, причем .

Ответ.

Интегрирование функций, рационально зависящих