КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегрирование рациональных дробей.
Теорема 6. Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором ее знаменатель не равен нулю, существует и выражается через элементарные функции, а именно рациональные дроби, логарифмы и арктангенсы.
Доказательство.
Представим рациональную дробь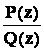 
в виде: 
. При этом последнее слагаемое является правильной дробью, и по теореме 5 ее можно представить в виде линейной комбинации простейших дробей. Таким образом, интегрирование рациональной дроби сводится к интегрированию многочлена S(x) и простейших дробей, первообразные которых, как было показано, имеют вид, указанный в теореме.
Замечание. Основную трудность при этом составляет разложение знаменателя на множители, то есть поиск всех его корней.
Пример 1. Найти интеграл 
Подынтегральная функция является правильной рациональной дробью. Разложение на неприводимые сомножители знаменателя имеет вид 
Это означает, что разложение подынтегральной функции в сумму простейших дробей имеет следующий вид:
Найдем коэффициенты разложения комбинированным методом:
Таким образом,
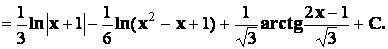
Дата добавления: 2015-04-18; просмотров: 68; Мы поможем в написании вашей работы!; Нарушение авторских прав |