Второй замечательный предел

В теории математического анализа доказано, что:

Данный факт носит название второго замечательного предела.

Справка: – это иррациональное число.

В качестве параметра может выступать не только переменная , но и сложная функция.Важно лишь, чтобы она стремилась к бесконечности.

Пример 6

Найти предел

Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.

Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение , по какому принципу это делается, разобрано на уроке Пределы. Примеры решений.

Нетрудно заметить, что при основание степени , а показатель – 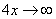, то есть имеется, неопределенность вида :

Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр 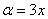, значит, в показателе нам тоже нужно организовать 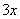. Для этого возводим основание в степень 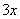, и, чтобы выражение не изменилось – возводим в степень :

Когда задание оформляется от руки, карандашом помечаем:

Практически всё готово, страшная степень превратилась в симпатичную букву :

При этом сам значок предела перемещаем в показатель:

Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.

Пример 7

Найти предел

Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример.

Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:

В результате получена неопределенность . Но второй замечательный предел применим к неопределенности вида . Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас 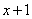, значит, в числителе тоже нужно организовать :

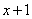Теперь можно почленно разделить числитель на знаменатель:

Вроде бы основание стало напоминать , но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:

Таким образом, основание приняло вид , и, более того, появилась нужная нам неопределенность . Организуем второй замечательный предел .
Легко заметить, что в данном примере . Снова исполняем наш искусственный прием: возводим основание степени в , и, чтобы выражение не изменилось – возводим в обратную дробь :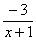

Наконец-то долгожданное устроено, с чистой совестью превращаем его в букву :