
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Непрерывность и точки разрыва. Предел функции в точке.
Определение 3.2 Точка  называется точкой разрыва функции
называется точкой разрыва функции  , если она определена в некоторой проколотой окрестности точки
, если она определена в некоторой проколотой окрестности точки  (то есть определена на некотором интервале, для которого
(то есть определена на некотором интервале, для которого  служит внутренней точкой, но в самой точке
служит внутренней точкой, но в самой точке  , возможно, не определена) и выполняется хотя бы одно из следующих условий:
, возможно, не определена) и выполняется хотя бы одно из следующих условий:
1) не существует предела слева  ;
;
2) не существует предела справа  ;
;
3) пределы слева 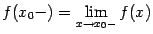 и справа
и справа  существуют, но не равны друг другу:
существуют, но не равны друг другу:  ;
;
4) пределы слева 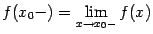 и справа
и справа  существуют и равны друг другу:
существуют и равны друг другу:  , но не совпадают со значением функции в точке
, но не совпадают со значением функции в точке  :
:  , или функция
, или функция  не определена в точке
не определена в точке  .
.
Если имеет место либо случай 3, либо случай 4, то точка разрыва  называетсяточкой разрыва первого рода, а поведение функции в окрестности точки
называетсяточкой разрыва первого рода, а поведение функции в окрестности точки  называетсяразрывом первого рода в точке
называетсяразрывом первого рода в точке  ; в случае 4 точка разрыва первого рода называетсяустранимой точкой разрыва, а разрыв функции в этой точке -- устранимым разрывом.
; в случае 4 точка разрыва первого рода называетсяустранимой точкой разрыва, а разрыв функции в этой точке -- устранимым разрывом.
Если же имеет место либо случай 1, либо случай 2 (либо и тот и другой сразу), то точка разрыва  называется точкой разрыва второго рода, а поведение функции в окрестности этой точки -- разрывом второго рода в точке
называется точкой разрыва второго рода, а поведение функции в окрестности этой точки -- разрывом второго рода в точке  .
.
Итак, если функция  имеет разрыв первого рода в точке
имеет разрыв первого рода в точке  , то существуют, как часто говорят, значения функции "на берегах разрыва":
, то существуют, как часто говорят, значения функции "на берегах разрыва":  и
и  , но точка
, но точка  не является точкой непрерывности.
не является точкой непрерывности.
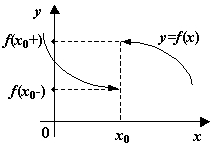
Рис.3.2.  -- точка разрыва первого рода
-- точка разрыва первого рода
Если значения на берегах разрыва разные, то значение функции в точке  может быть любым (или вообще отсутствовать), всё равно
может быть любым (или вообще отсутствовать), всё равно  будет давать разрыв первого рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке
будет давать разрыв первого рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке  , либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию
, либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию  в точке
в точке  , положив
, положив  , то полученная изменённая функция будет уже непрерывна в точке
, то полученная изменённая функция будет уже непрерывна в точке  и разрыв в точке
и разрыв в точке  исчезнет; отсюда и название такого разрыва -- устранимый.
исчезнет; отсюда и название такого разрыва -- устранимый.
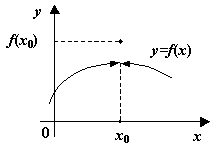
Рис.3.3.  -- точка устранимого разрыва
-- точка устранимого разрыва
Наконец, к разрывам второго рода, как видно из определения, относятся все разрывы, которые не принадлежат к разрывам первого рода; некоторые из возможных способов поведения функции в окрестности точки  , где происходит разрыв второго рода, представлены на следующем рисунке.
, где происходит разрыв второго рода, представлены на следующем рисунке.


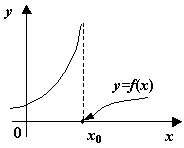
Рис.3.4.  -- точка разрыва второго рода. Некоторые возможные варианты
-- точка разрыва второго рода. Некоторые возможные варианты
Пример 3.3 Рассмотрим функцию  , для которой
, для которой
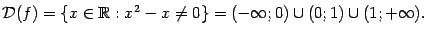
Функция имеет разрывы при  и при
и при  . Нетрудно видеть, что при
. Нетрудно видеть, что при 
 В точках
В точках  и
и  функция имеет неустранимые разрывы первого рода. В точке
функция имеет неустранимые разрывы первого рода. В точке  имеем:
имеем:
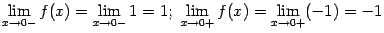
(значения на краях разыва существуют, но не совпадают); в точке  --
--
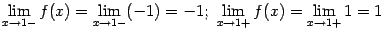
(снова пределы слева и справа существуют, но не совпадают).
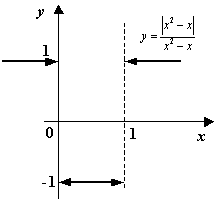
Рис.3.5.График функции 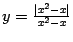
Дата добавления: 2015-04-18; просмотров: 271; Мы поможем в написании вашей работы!; Нарушение авторских прав |