КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
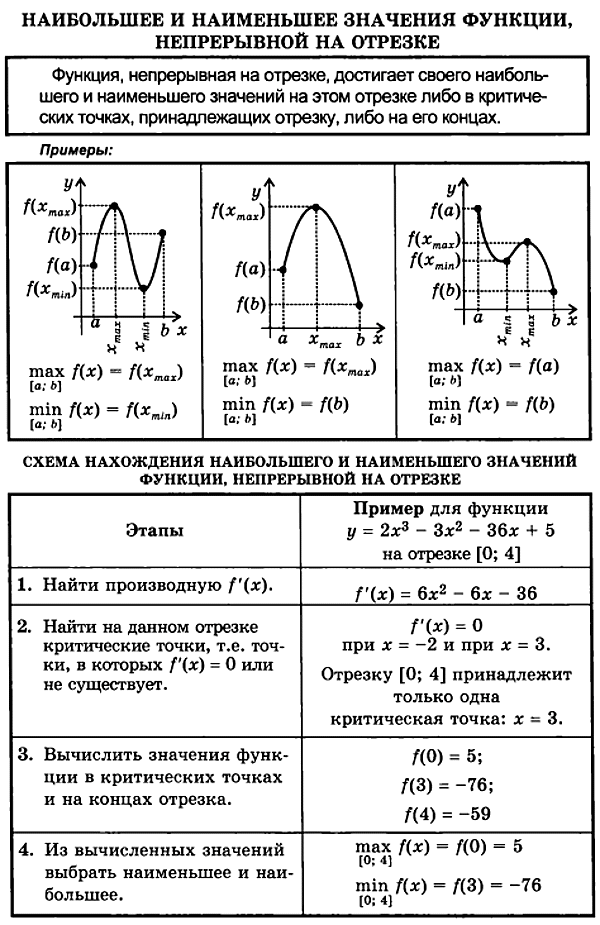
Исследование функции с помощью производной.
22. Геометрический смысл производной.
Тангенс угла наклона касательной (угловой коэффициент наклона касательной), проведенной к графику функции
в точке 
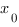равен производной функции в этой точке:
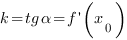
Заметим, что угол 
– это угол между прямой и положительным направлением оси ОХ:
Уравнение касательной к графику функции в точке 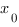имеет вид:
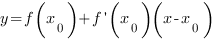
В этом уравнении:
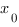– абсцисса точки касания,
– значение функции в точке касания,
– значение производной функции в точке касания.
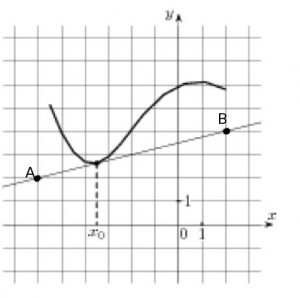
Пример1.Задание В8 (№ 27504) На рисунке изображены график функции и касательная к нему в точке с абcцисcой 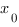. Найдите значение производной функции в точке .
Значение производной функции в точке 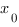равно тангенсу угла между касательной и положительным направлением оси ОХ.Чтобы его найти, выделим прямоугольный треугольник, гипотенуза которого лежит на касательной, а катеты параллельны осям координат. Обозначим точки с целыми координатами буквами А и В – эти точки выделены на касательной:
Проведем через точку А прямую параллельно оси ОХ, а через точку В – параллельно оси OY. Получим прямоугольный треугольник ABC:
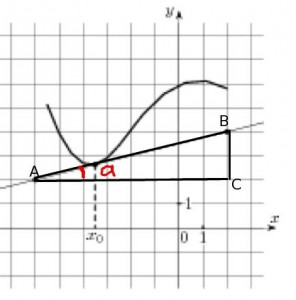
Угол А треугольника АВС равен углу между касательной и положительным направлением оси ОХ.
Дата добавления: 2015-04-18; просмотров: 166; Мы поможем в написании вашей работы!; Нарушение авторских прав |