
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Неопределенный интеграл и его свойства
Неопределенным интегралом называют не только множество всех первообразных, но и любую функцию этого множества. Таким образом, неопределенный интеграл представляет собой любую функцию, дифференциал которой равен подинтегральному выражению, а производная равна подинтегральной функции
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,
а, k, C - постоянные величины.
1) производная от неопределенного интеграла равна подинтегральной функции
( ∫f(x)dx)’=f(x)
2) дифференциал неопределенного интеграла равен поинтегральному выражению
D (∫f(x)dx)=f(x)dx
3) неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого.
∫d F(x)=F(x)+C
4) Постоянный множитель можно выносить за знак интеграла
∫ɑf(x)dx=ɑ∫f(x)dx
5) Интеграл от алгебраической суммы 2-х функций равен такой же сумме интегралов от этих же функций

Таблица интегралов
В формулах ниже предполагается, что a, p (p ≠ 1), C - действительные постоянные, b - основание показательной функции (b ≠ 1, b > 0).

| 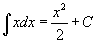
|

| 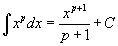
|

| 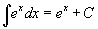
|
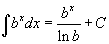
| 
|
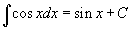
| 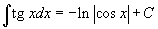
|

|
Дата добавления: 2015-04-18; просмотров: 258; Мы поможем в написании вашей работы!; Нарушение авторских прав |