Основные теоремы о пределах

Теорема 1.(о единственности предела функции). Функция не может иметь более одного предела.

Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки 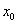, за исключением, может быть, самой точки 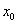, то либо они имеют один и тот же предел при 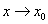, либо обе не имеют предела в этой точке.

Теорема 2.Если функцииf(x) и g(x) имеют пределы в точке 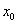, то:

1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых,т.е.

(2)

2) предел произведения функций равен произведению пределов сомножителей, т.е.

(3)

3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю,т.е.

(4)

Замечание.Формулы (2) и (3) справедливы для любого конечного числа функций.

Следствие 1.Предел постоянной равен самой постоянной, т.е.

Следствие 2.Постоянный множитель можно выносить за знак предела, т.е.

Теорема 3(о пределе сложной функции). Если существует конечный предел

а функцияf(u) непрерывна в точке , то

Другими словами, для непрерывных функций символы предела и функции можно поменять местами.

Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.