КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доказательство. Пусть существуют такие, что
Пусть существуют 
такие, что 
. Функция 
непрерывна на отрезке 
, так как она дифференцируема на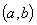 
и 
. Тогда 
, т.е. дифференцируема и на 
. Значит, по теореме Лагранжа, 
. Так как всегда 
, то значение 
непосредственно зависит от значения производной. То есть знак функции совпадает со знаком производной.
Теорема 18.4 (Третье следствие теоремы Лагранжа)
Пусть X - некоторый промежуток, и значения производной на этом промежутке ограничены числом C: 
. Тогда функция равномерно непрерывна на данном промежутке.
Доказательство
Требуется доказать, что 
(см. определение равномерной непрерывности - п. 13). По теореме Лагранжа имеем: 
. Обозначив 
, получаем: 
.
Пример: функция 
, имеющая ограниченную производную 
, 
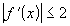. Данная функция действительно является равномерно непрерывной.
Дата добавления: 2015-04-18; просмотров: 56; Мы поможем в написании вашей работы!; Нарушение авторских прав |