
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Условия существования предела функции комплексного переменного
Утверждение 2.3 (необходимое и достаточное условие существования предела функции комплексного переменного).
Для того чтобы в точке  существовал предел функции
существовал предел функции 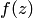 , необходимо и достаточно, чтобы в точке
, необходимо и достаточно, чтобы в точке  существовали пределы двух функций действительных переменных
существовали пределы двух функций действительных переменных 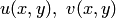 , где
, где  ; при этом имеет место равенство
; при этом имеет место равенство
18. Наибольшие и наименьшие значения функции.
Если функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке  , то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение
, то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение  функция
функция  принимает в точке
принимает в точке  , то
, то  будет локальным максимумом функции
будет локальным максимумом функции  , так как в этом случае существует окрестность точки
, так как в этом случае существует окрестность точки  , такая, что
, такая, что  .
.
Однако свое наибольшее значение  функция
функция  может принимать и на концах отрезка
может принимать и на концах отрезка  . Поэтому, чтобы найти наибольшее значение
. Поэтому, чтобы найти наибольшее значение  непрерывной на отрезке
непрерывной на отрезке  функции
функции  , надо найти все максимумы функции на интервале
, надо найти все максимумы функции на интервале  и значения
и значения  на концах отрезка
на концах отрезка  , то есть
, то есть  и
и 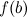 , и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.
, и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.
Наименьшим значением  непрерывной на отрезке
непрерывной на отрезке  функции
функции  будет наименьший минимум среди всех минимумов функции
будет наименьший минимум среди всех минимумов функции  на интервале
на интервале  и значений
и значений  и
и 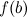 .
.
Пример
Задание. Найти наибольшее и наименьшее значение функции 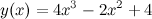 на отрезке
на отрезке 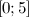 .
.
Решение. Находим производную функции:

Находим точки, в которых производная равна нулю:

Из полученных значений нам надо оставить лишь те, которые принадлежат заданному промежутку 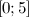 . Оба значения лежат в этом промежутке.
. Оба значения лежат в этом промежутке.
Находим значения функции в полученных стационарных точках из промежутка и на концах промежутка:

Таким образом,
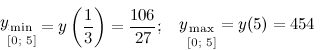
Ответ. 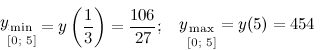
Дата добавления: 2015-04-18; просмотров: 275; Мы поможем в написании вашей работы!; Нарушение авторских прав |