Асимптоты графика функции

Асимптота – это прямая, к которой бесконечно близко приближается график функции, при этом он должен бесконечно далеко удаляться от начала координат.

Примечание: определение содержательно, если вам необходима формулировка в терминах и обозначениях математического анализа, пожалуйста, обратитесь к учебнику.

На плоскости асимптоты классифицируют по их естественному расположению:

1) Вертикальные асимптоты, которые задаются уравнением вида 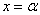, где «альфа» – действительное число. Популярная представительница определяет саму ось ординат, вспоминаем гиперболу .

2) Наклонные асимптоты традиционно записываются уравнением прямой с угловым коэффициентом . Иногда отдельной группой выделяют частный случай –горизонтальные асимптоты . Например, та же гипербола с асимптотой .

Пример 1

Найти асимптоты графика функции

Решение удобно разбить на два пункта:

1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при , и сразу понятно, что в данной точке функция терпит бесконечный разрыв, а прямая, заданная уравнением , является вертикальной асимптотой графика функции . Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:

Напоминаю технику вычислений, на которой я подобно останавливался в статьеНепрерывность функции. Точки разрыва. В выражение под знаком предела вместо «икса» подставляем . В числителе ничего интересного:
.

А вот в знаменателе получается бесконечно малое отрицательное число:
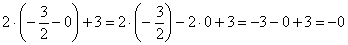, оно и определяет судьбу предела.

Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого – они ПОМОГАЮТ ПОНЯТЬ, КАКрасположен график функции и построить егоКОРРЕКТНО. Поэтому обязательно вычислим и правосторонний предел:

Вывод: односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при .

15. Замечательные пределы