
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
От тригонометрических функций
Символом R(x) будем обозначать рациональные функции от х. Запись R(sinx, cosx) обозначает, что функция рациональная относительно как синуса, так и косинуса.
Основная идея всех приведенных ниже подстановок состоит в том, что они сводят вычисление интеграла к интегралу от рациональных дробей.
Общий случай. Рассмотрим интеграл вида 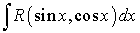 и покажем, что этот интеграл с помощью подстановки
и покажем, что этот интеграл с помощью подстановки 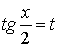 всегда сводится к интегралу от рациональной функции и, значит, такие интегралы выражаются в конечном виде через элементарные. Сделаем подстановку:
всегда сводится к интегралу от рациональной функции и, значит, такие интегралы выражаются в конечном виде через элементарные. Сделаем подстановку:
 ;
; 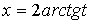 ;
;  ;
;
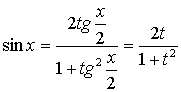 ;
; 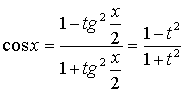 .
.
Таким образом, sin x, cos x, dx выражаются рационально через t. А так как рациональная функция от рациональной есть функция рациональная, то, подставляя полученные выражения в интеграл, найдем интеграл от рациональной функции:
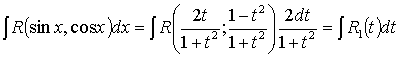 .
.
Эту подстановку называют универсальной тригонометрической подстановкой.
П р и м е р 11. Найти интеграл 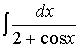 .
.
Решение. 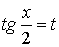 ,
, 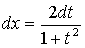 ,
,  .
.
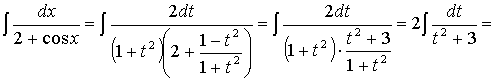

 .
.
Но универсальная тригонометрическая подстановка часто приводит к громоздким вычислениям. Поэтому надо знать другие подстановки и приёмы, которые в некоторых частных случаях быстрее приводят к цели.
Частные случаи. 1. Если имеет место тождество
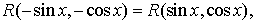
то для приведения интеграла 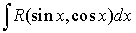 к рациональному виду рекомендуется применять подстановку
к рациональному виду рекомендуется применять подстановку 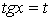 .
.
Тогда 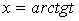 ,
, 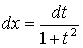 ,
, 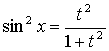 ,
, 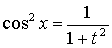 .
.
В частности, указанное выше тождество выполняется, если функции 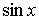 и
и 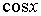 входят только в четных степенях, т. е.
входят только в четных степенях, т. е. 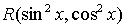 . Тогда после подстановки получим
. Тогда после подстановки получим
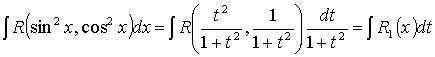 .
.
Такую же подстановку применяют при вычислении интегралов вида
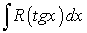 .
.
Замечание. Интеграл от 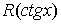 сводится к интегралу
сводится к интегралу  , т. к.
, т. к. 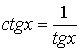 .
.
4. Интегралы вида  ,
, 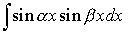 ,
, 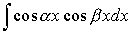
 легко вычисляются после применения известных формул тригонометрии
легко вычисляются после применения известных формул тригонометрии
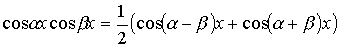 ;
;
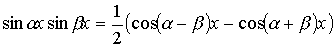 ;
;
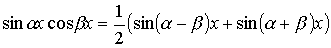 .
.
Дата добавления: 2015-04-18; просмотров: 226; Мы поможем в написании вашей работы!; Нарушение авторских прав |