Определенный интеграл. Основные свойства определенного интеграла.

Определенный интеграл:

y=f(x), x=a, x=b, Ox

S_n≈S, S_n→S, n→∞

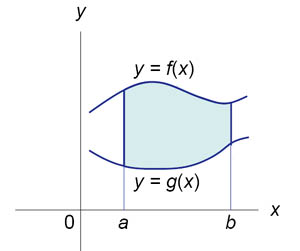
Фигура ABCD, ограниченная сверху графиком функции y=f(x), с 2-х боковых сторон прямыми х=а, х=в, а снизу-осью Ох называется криволинейной трапецией.

Отрезок ab-основание криволинейной трапеции

Сумма площадей n-прямоугольников, составляющая S криволинейной трапеции.

Сумма площадей этих прямоугольников-определенный интеграл

S=_a∫^b f(x)dx

Определенный интеграл — это аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых — интегрируемая функция или функционал, а вторая — область во множестве задания этой функции.
Проще говоря, это интеграл, численно равный площади части графика функции в пределах от a до b, т. е. площади криволинейной трапеции.

Пример.

Вычислить определенный интеграл

Решение:

(1) Выносим константу за знак интеграла.

(2) Интегрируем по таблице с помощью самой популярной формулы . Появившуюся константу целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?

(3) Используем формулу Ньютона-Лейбница . Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.

Основные свойства определенного интеграла.

1. где k - константа;

Если k-постоянное число и функция f(x), интегрируемая на отрезке [a;b], то постоянный множитель можно выносить за знак ∫

2. _a∫^b (f₁(x)+f₂(x))dx= _a∫^b (f₁(x)dx+= _a∫^b f₂(x)dx

3.

4.

Если f(x) [a;b] и a<c<b, то ∫ по всему отрезку равен ∑е ∫-ов по частям этого отрезка. Это свойство называется свойством аддитивности.

5. Если f(x) непрерывна на самом [a;b], то существует а с принадлежащим [a;b] такая, что

_a∫^b (f(x)dx=f(c) (b-a)

Теорема «о среднем»

F(c)=1/b-a _a∫^b (f(x)dx-это число называется средним значением функции f(x) на [a;b]

6. Если f(x) сохраняет знак на [a;b], где a,b, то _a∫^b (f(x)dx имеет тот же знак, что и функция

Если f(x) ≥0 на [a;b], то _a∫^b (f(x)dx≥0

7. Неравенство между непрерывными функциями на [a;b] (a>b) можно проинтегрировать т.к. f₁(x)≤0 f₂(x) при x€[a;b], то:

_a∫^bf₁(x) ≤ _a∫^bf₂(x)dx

8. оценка интегралов

Если m и M – соответственно наименьшее и наибольшее значение функции y=f(x) на [a;b], (a;b), то:

m(b-a)≤ _a∫^bf(x)dx≤M(b-a)

9. Модуль определенного интеграла не превосходит интеграла от модуля подинтегральной функции.

│ _a∫^bf(x)dx │ ≤ _a∫^{b │}f(x)dx│

10. Производная определенного интеграла по переменному значению верхнего предела равна подинтегральной функции, которой переменная интегрирования заменена этим пределом:

( _a∫^bf(t)dt)’_x=f(x)