
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Принцип полной математической индукции
Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений 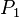 , , 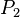 , , 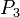 , , 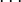 . Если для любого натурального . Если для любого натурального 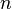 из того, что истинны все из того, что истинны все 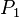 , , 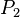 , , 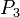 , , 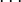 , , 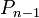 , следует также истинность , следует также истинность 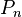 , то все утверждения в этой последовательности истинны, то есть , то все утверждения в этой последовательности истинны, то есть  . .
|
В этой вариации база индукции оказывается излишней, поскольку является тривиальным частным случаем индукционного перехода. Действительно, при 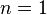 импликация
импликация 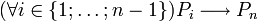 эквивалентна
эквивалентна 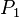 . Принцип полной математической индукции является прямым применением более сильной трансфинитной индукции.
. Принцип полной математической индукции является прямым применением более сильной трансфинитной индукции.
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.
Пример.
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
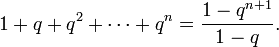
Доказательство. Индукция по n.
База, n = 1:
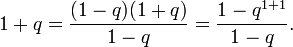
Переход: предположим, что
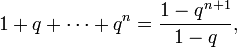
тогда
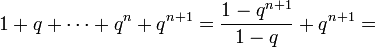
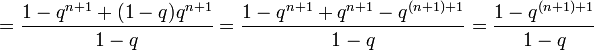 ,
,
что и требовалось доказать.
Комментарий: верность утверждения 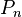 в этом доказательстве — то же, что верность равенства
в этом доказательстве — то же, что верность равенства
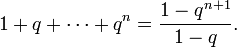
Дата добавления: 2015-04-18; просмотров: 243; Мы поможем в написании вашей работы!; Нарушение авторских прав |