
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие последовательности и ее предел.
Последовательность — это функция натурального аргумента.
Последовательности вида:

принято компактно записывать при помощи круглых скобок:
 или
или 
иногда используются фигурные скобки:
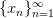 .
.
Пример: числовые последовательности:
1) 1,2,…, n,…;
2) 1,-1,1,-1,…,(-1)n,…;
3) 1,1/2,1/3,…,1/n,….
Опр. Числоа называется пределом последовательности  , если для каждого
, если для каждого  >0 существует такой номер
>0 существует такой номер 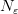 , что для всех
, что для всех  выполняется неравенство:
выполняется неравенство:

Если а — предел последовательности, то пишут:  ...
...
Последовательность, у которой существует предел, называют сходящейся.
Последовательность называют расходящейся, если никакое число не является ее пределом.
Из определения следует, что последовательность  имеет предел, равный а, тогда и только тогда, когда последовательность
имеет предел, равный а, тогда и только тогда, когда последовательность  имеет предел, равный нулю, т. е.:
имеет предел, равный нулю, т. е.:

Пример: Пользуясь определением, найти предел последовательности  , если:
, если:
 .
.
решение:
Докажем, что 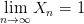 . Так как
. Так как  , то
, то  . Возьмем произвольное число
. Возьмем произвольное число  . Неравенство
. Неравенство  будет выполняться, если
будет выполняться, если  . Выберем в качестве
. Выберем в качестве 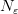 какое-нибудь натуральное число, удовлетворяющее условию
какое-нибудь натуральное число, удовлетворяющее условию  , например, число
, например, число  . Тогда для всех
. Тогда для всех 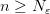 будет выполняться неравенство
будет выполняться неравенство  . По определению предела это означает, что
. По определению предела это означает, что 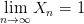 .
.
Дата добавления: 2015-04-18; просмотров: 214; Мы поможем в написании вашей работы!; Нарушение авторских прав |